题目内容
直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:
(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把极坐标方程、参数方程化为直角坐标方程,根据圆和圆的位置关系,求出|AB|的最小值.
解答:
解:把曲线C1:
(θ为参数)化为普通方程为 (x-3)2+y2=9,
表示以(3,0)为圆心,半径等于3的圆.
曲线C2:ρ=1,即 x2+y2=1,表示以原点为圆心、半径等于1的圆,
故两圆的圆心距d=3,则|AB|的最小值为 1,
故单答案为:1.
|
表示以(3,0)为圆心,半径等于3的圆.
曲线C2:ρ=1,即 x2+y2=1,表示以原点为圆心、半径等于1的圆,
故两圆的圆心距d=3,则|AB|的最小值为 1,
故单答案为:1.
点评:本题主要考查把极坐标方程、参数方程化为直角坐标方程的方法,圆和圆的位置关系,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
若抛物线的焦点是双曲线
-
=1的一个焦点,顶点是坐标原点,则抛物线的标准方程是( )
| y2 |
| 5 |
| x2 |
| 4 |
| A、y2=±4x |
| B、y2=12x |
| C、x2=±12y |
| D、x2=12y |
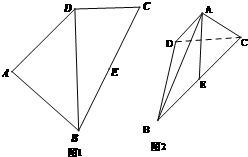 如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=
如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=