题目内容
已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为坐标原点O,从每条曲线上各取两个点,将其坐标记录于表中:
(Ⅰ)求C1、C2的标准方程;
(Ⅱ)请问是否存在直线l同时满足条件:(ⅰ)过C2的焦点F;(ⅱ)与C1交于不同两点Q、R,且满足
⊥
?若存在,求出直线l的方程;若不存在,请说明理由;
(Ⅲ)已知椭圆C1的左顶点为A,过A作两条互相垂直的弦AM、AN分别另交椭圆于M、N两点.当直线AM的斜率变化时,直线MN是否过x轴上的一定点,若过定点,请给出证明,并求出该定点坐标;若不过定点,请说明理由.
| x | 3 | -2 | 4 |
| ||||||
| y | -2
| 0 | -4 |
|
(Ⅱ)请问是否存在直线l同时满足条件:(ⅰ)过C2的焦点F;(ⅱ)与C1交于不同两点Q、R,且满足
| OQ |
| OR |
(Ⅲ)已知椭圆C1的左顶点为A,过A作两条互相垂直的弦AM、AN分别另交椭圆于M、N两点.当直线AM的斜率变化时,直线MN是否过x轴上的一定点,若过定点,请给出证明,并求出该定点坐标;若不过定点,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设抛物线C2:y2=2mx(m≠0),则有
=2m,据此验证4个点知:(3,-2
),(4,-4)在抛物线上,即可得出C2:y2=4x.
设C1:
+
=1(a>b>0),把点(-2,0),(
,
)代入解出即可.
(II)验证直线l的斜率不存在时,不满足题意;当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),设其方程为y=k(x-1),与C1的交点坐标为Q(x1,y1),R(x2,y2).把直线方程与椭圆方程联立可得(1+4k2)x2-8k2x+4(k2-1)=0,得到根与系数的关系,由
⊥
,kd
•
=x1x2+y1y2=0,把根与系数的关系代入解得k即可得出.
(III)设直线AM的斜率为k(k≠0),则AM:y=k(x+2),AN:y=-
(x+2).f分别与椭圆的方程联立可得xM,yM.xN,yN.k可得MN的直线方程为y-
=
(x-
),令y=0,解出即可.
| y2 |
| x |
| 3 |
设C1:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(II)验证直线l的斜率不存在时,不满足题意;当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),设其方程为y=k(x-1),与C1的交点坐标为Q(x1,y1),R(x2,y2).把直线方程与椭圆方程联立可得(1+4k2)x2-8k2x+4(k2-1)=0,得到根与系数的关系,由
| OQ |
| OR |
| OQ |
| OR |
(III)设直线AM的斜率为k(k≠0),则AM:y=k(x+2),AN:y=-
| 1 |
| k |
| 4k |
| 1+4k2 |
| -5k |
| 4(k2-1) |
| 2-8k2 |
| 1+4k2 |
解答:
解:(Ⅰ)设抛物线C2:y2=2mx(m≠0),则有
=2m,据此验证4个点知:(3,-2
),(4,-4)在抛物线上,
可得C2:y2=4x.
设C1:
+
=1(a>b>0),把点(-2,0),(
,
)代入得:
,解得
,
∴C1的方程为
+y2=1.
(Ⅱ)验证直线l的斜率不存在时,不满足题意;
当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),设其方程为y=k(x-1),与C1的交点坐标为Q(x1,y1),R(x2,y2).
由
消去y,得(1+4k2)x2-8k2x+4(k2-1)=0,
于是x1+x2=
,x1x2=
,…①
y1y2=k2(x1-1)(x2-1)=k2[x1x2-(x1+x2)+1]=k2[
-
+1]=
,…②
由
⊥
,∴
•
=x1x2+y1y2=0(*),
将①、②代入(*)式,得
-
=
=0,解得k=±2;
∴存在直线l满足条件,且l的方程为:y=2x-2或y=-2x+2.
(Ⅲ)设直线AM的斜率为k(k≠0),则AM:y=k(x+2),AN:y=-
(x+2).
则
化简得:(1+4k2)x2+16k2x+16k2-4=0.
∵此方程有一根为-2,∴xM=
,yM=
.
同理可得xN=
,yN=
,
则kMN=
=
.
∴MN的直线方程为y-
=
(x-
),
令y=0,则x=
+
=-
.
∴直线MN过x轴上的一定点(-
,0).
| y2 |
| x |
| 3 |
可得C2:y2=4x.
设C1:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
|
|
∴C1的方程为
| x2 |
| 4 |
(Ⅱ)验证直线l的斜率不存在时,不满足题意;
当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),设其方程为y=k(x-1),与C1的交点坐标为Q(x1,y1),R(x2,y2).
由
|
于是x1+x2=
| 8k2 |
| 1+4k2 |
| 4(k2-1) |
| 1+4k2 |
y1y2=k2(x1-1)(x2-1)=k2[x1x2-(x1+x2)+1]=k2[
| 4(k2-1) |
| 1+4k2 |
| 8k2 |
| 1+4k2 |
| -3k2 |
| 1+4k2 |
由
| OQ |
| OR |
| OQ |
| OR |
将①、②代入(*)式,得
| 4(k2-1) |
| 1+4k2 |
| 3k2 |
| 1+4k2 |
| k2-4 |
| 1+4k2 |
∴存在直线l满足条件,且l的方程为:y=2x-2或y=-2x+2.
(Ⅲ)设直线AM的斜率为k(k≠0),则AM:y=k(x+2),AN:y=-
| 1 |
| k |
则
|
∵此方程有一根为-2,∴xM=
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
同理可得xN=
| 2k2-8 |
| k2+4 |
| -4k |
| k2+4 |
则kMN=
| yN-yM |
| xN-xM |
| -5k |
| 4(k2-1) |
∴MN的直线方程为y-
| 4k |
| 1+4k2 |
| -5k |
| 4(k2-1) |
| 2-8k2 |
| 1+4k2 |
令y=0,则x=
| 16k(k2-1) |
| 5k(1+4k2) |
| 2-8k2 |
| 1+4k2 |
| 6 |
| 5 |
∴直线MN过x轴上的一定点(-
| 6 |
| 5 |
点评:本题考查了椭圆与抛物线的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、相互垂直与斜率的关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=
,则f[f(3)]=( )
|
| A、-3 | B、3 | C、-9 | D、9 |
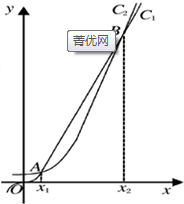 函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.
函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.