题目内容
2.已知(2,0)是双曲线${x^2}-\frac{y^2}{b^2}=1$的一个焦点,则b=±$\sqrt{3}$.分析 根据题意,由双曲线焦点的坐标,分析可得c的值,进而由双曲线的几何性质可得1+b2=4,解可得b的值.
解答 解:根据题意,双曲线${x^2}-\frac{y^2}{b^2}=1$的一个焦点为(2,0),
即其焦点在x轴上,且c=2,
则有1+b2=4,
解可得b=±$\sqrt{3}$;
故答案为:±$\sqrt{3}$.
点评 本题考查双曲线的几何性质,关键是分析焦点位置.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
10.若函数f(x)=x2-4x+a对于一切x∈[0,1]时,恒有f(x)≥0成立,则实数a的取值范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | (-∞,3] | D. | (-∞,3) |
11.化简$\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BD}-\overrightarrow{CD}$=( )
| A. | 0 | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{DA}$ | D. | $\overrightarrow 0$ |
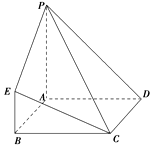 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.