题目内容
12.已知双曲线C:$\frac{x^2}{a^2}-4{y^2}=1({a>0})$的右顶点到其一条渐近线的距离等于$\frac{{\sqrt{3}}}{4}$,抛物线E:y2=2px的焦点与双曲线C的右焦点重合,则抛物线E上的动点M到直线l1:4x-3y+6=0和l2:x=-1的距离之和的最小值为2.分析 求出双曲线的渐近线方程,运用点到直线的距离公式计算可得a,进而得到c,由抛物线的焦点坐标,可得p=2,进而得到抛物线的方程.连接MF,过点M作MA⊥l1于点A,作MB⊥准线x=-1于点C.由抛物线的定义,得到d1+d2=MA+MF,再由平面几何知识可得当M、A、F三点共线时,MA+MF有最小值,因此算出F到直线l的距离,即可得到所求距离的最小值.
解答 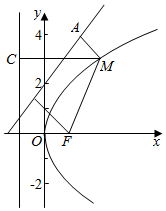 解:双曲线C:$\frac{x^2}{a^2}-4{y^2}=1({a>0})$的渐近线方程为y=±$\frac{x}{2a}$,
解:双曲线C:$\frac{x^2}{a^2}-4{y^2}=1({a>0})$的渐近线方程为y=±$\frac{x}{2a}$,
右顶点(a,0)到其一条渐近线的距离等于$\frac{{\sqrt{3}}}{4}$,
可得$\frac{a}{\sqrt{1+4{a}^{2}}}$=$\frac{{\sqrt{3}}}{4}$,
解得a=$\frac{{\sqrt{3}}}{4}$,
即有c=1,
由题意可得$\frac{p}{2}$=1,解得p=2,
即有抛物线的方程为y2=4x,
如图,过点M作MA⊥l1于点A,
作MB⊥准线l2:x=-1于点C,
连接MF,根据抛物线的定义得MA+MC=MA+MF,
设M到l1的距离为d1,M到直线l2的距离为d2,
∴d1+d2=MA+MC=MA+MF,
根据平面几何知识,可得当M、A、F三点共线时,MA+MF有最小值.
∵F(1,0)到直线l1:4x-3y+6=0的距离为$\frac{|4-0+6|}{\sqrt{16+9}}$=2.
∴MA+MF的最小值是2,
由此可得所求距离和的最小值为2.
故答案为2.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,同时考查抛物线的方程和性质,给出抛物线和直线l1,求抛物线上一点到准线的距离与直线l1距离之和的最小值,着重考查了点到直线的距离公式、抛物线的定义和简单几何性质等知识,属于中档题.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| A. | $\frac{3+i}{2}$ | B. | $\frac{1+3i}{2}$ | C. | $\frac{1+i}{2}$ | D. | $\frac{3+2i}{2}$ |
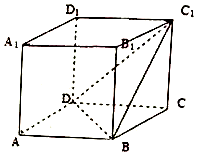 在直四棱柱ABCD-A1B1C1D1中,AB=4,AA1=2$\sqrt{3}$,底面ABCD为菱形,且∠BAD=60°.
在直四棱柱ABCD-A1B1C1D1中,AB=4,AA1=2$\sqrt{3}$,底面ABCD为菱形,且∠BAD=60°.