题目内容
8.已知全集U=R,若集合A={y|y=3-2-x},B={x|$\frac{x-2}{x}$≤0},则A∩∁UB=( )| A. | (-∞,0)∪[2,3) | B. | (-∞,0]∪(2,3) | C. | [0,2) | D. | [0,3) |
分析 由指数函数的值域求出集合A,由分式不等式的解法求出集合B,由补集的运算求出∁UB,由交集的运算求出A∩∁UB.
解答 解:由2-x>0得y=3-2-x<3,则A={y|y=3-2-x}=(-∞,3),
由$\frac{x-2}{x}≤0$得$\left\{\begin{array}{l}{x(x-2)≤0}\\{x≠0}\end{array}\right.$,解得0<x≤2,则B=(0,2],
又U=R,则∁UB=(-∞,0]∪(2,+∞),
所以A∩∁UB=(-∞,0]∪(2,3),
故选:B.
点评 本题考查了交、并、补集的混合运算,指数函数的值域,以及分式不等式的解法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知函数$f(x)=\left\{\begin{array}{l}1-{2^x},x≤0\\{log_2}x,x>0\end{array}\right.$,则f(f(-1))=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
16.在极坐标系中,点(1,0)与点(2,π)的距离为( )
| A. | 1 | B. | 3 | C. | $\sqrt{1+{π^2}}$ | D. | $\sqrt{9+{π^2}}$ |
17.曲线y=-$\frac{1}{x}$在(1,-1)处的切线的斜率为( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
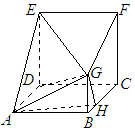 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH