题目内容

已知直线l在y轴上的截距为2且倾斜角为45°，则直线l方程为
 
；若圆C的圆心为（-2，2），且与直线l相切，则圆C方程是为
 
．
考点：圆的标准方程,直线的截距式方程
专题：计算题,直线与圆
分析：①先求出直线的斜率，进而利用斜截式即可求出；
②先由已知条件求出圆的半径，进而利用圆的标准方程即可得出．
解答： 解：∵直线l倾斜角为45°，∴斜率k=tan45°=1，∴直线l的方程为y=x+2，
∵所求的圆是以点（-2，2）为圆心且与直线l相切，∴半径r=
2
．
∴圆的方程为（x+2）2+（y-2）2=2．
故答案为y=x+2；（x+2）2+（y-2）2=2．
点评：熟练掌握直线方程的四种形式和圆的标准方程是解题的关键．
练习册系列答案
相关题目
如图的三视图表示的几何体是（　　）
A、圆台B、棱锥C、圆锥D、圆柱
若x，y满足
y-1≥0
2x-y-1≥0
x+y≤m
，若目标函数z=x-y的最小值为-2，则实数m的值为
 
．
下列不等关系中，正确的是（　　）
A、（
1
2
） 
2
3
＜1＜（
1
2
） 
1
3
B、（
1
2
） 
1
3
＜（
1
2
） 
2
3
＜1
C、1＜（
1
2
） 
1
3
＜（
1
2
） 
2
3
D、（
1
2
） 
2
3
＜（
1
2
） 
1
3
＜1
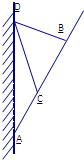某固定在墙上的广告金属支架如图所示，根据要求，AB至少长3米，C为AB的中点，B到D的距离比CD的长小0.5米，∠BCD=60°
（1）若CD=x，BC=y，将支架的总长度表示为y的函数，并写出函数的定义域．（注：支架的总长度为图中线段AB、BD和CD长度之和）
（2）如何设计AB，CD的长，可使支架总长度最短．
函数y=2x+
1
x
（x＞0）的最小值为（　　）
A、2
B、2
2
C、4
D、4
2
已知
C
x+3
15
=
C
2x
15
，求x的值．
已知a∈R，解关于x的不等式：x2+（a+1）x+a＜0．
函数y=
2x+1
+
3-4x
的定义域为（　　）
A、(-
1
2
，
3
4
)
B、[-
1
2
，
3
4
]
C、(-∞，
1
2
]∪[
3
4
，+∞)
D、(-
1
2
，0)∪(0，+∞)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网