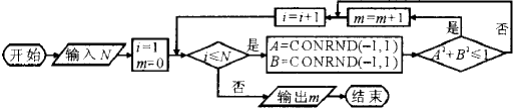
题目内容
已知二项展开式(1+ax)5=1+a1x+a2x2+a3x3+a4x4+a5x5,集合A={80,40,32,10},若ai∈A(i=1,2,3,4,5),则a= .
考点:二项式定理的应用
专题:计算题,集合,二项式定理
分析:运用二项式定理展开,可得对应项的系数,再由条件判断a>1,对a1讨论,即可得到所求值.
解答:
解:由二项式定理,可得,
(1+ax)5=1+
ax+
a2x2+
a3x3+
a4x4+
a5x5,
则有a1=5a,a2=10a2,a3=10a3,a4=5a4,a5=a5.
由于集合A={80,40,32,10},且ai∈A(i=1,2,3,4,5),
则ai>0,即a>0,若a=1,则显然不成立,即a>1,则a1为较小的,
若a1=32或40,则显然不成立,若a1=10,则a=2,
a1=10,a2=40,a3=80,a4=80,a5=32.成立.
故答案为:2.
(1+ax)5=1+
| C | 1 5 |
| C | 2 5 |
| C | 3 5 |
| C | 4 5 |
| C | 5 5 |
则有a1=5a,a2=10a2,a3=10a3,a4=5a4,a5=a5.
由于集合A={80,40,32,10},且ai∈A(i=1,2,3,4,5),
则ai>0,即a>0,若a=1,则显然不成立,即a>1,则a1为较小的,
若a1=32或40,则显然不成立,若a1=10,则a=2,
a1=10,a2=40,a3=80,a4=80,a5=32.成立.
故答案为:2.
点评:本题考查二项式定理的运用,考查元素和集合的关系,考查推断能力和运算能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
已知函数f(x)=ax3+bx+4(a,b∈R),f(lg(log210))=5,则f[lg(lg2)]=( )
| A、-3 | B、-1 | C、3 | D、4 |
某几何体的三视图(单位:cm)如图所示,则该几何体的体积为:( )
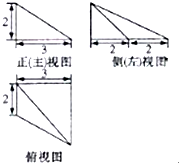

| A、2cm2 | ||
B、
| ||
C、
| ||
| D、6cm2 |