题目内容
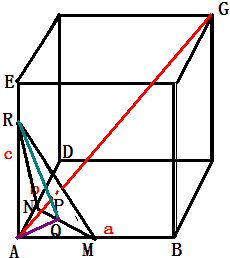
在平行六面体ABCD-EFGH中,已知M、N、R分别是AB、AD、AE上的点,且AM=MB,AN=
ND,AR=2RE,求平面MNR分对角线AG所得线段AP与PG的比.
| 1 |
| 2 |
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:设出
,
,
,
=2
+3
+
,
=kAG=k(2AM+3AN+
AR)=2kAM+3kAN+
kAR,由此能求出AP:PG=2:11.
| AM |
| AN |
| AR |
| AG |
| AM |
| AN |
| 3 |
| 2 |
| AR |
| AP |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:设出
,
,
,
∵M、N、R分别是AB、AD、AE上的点,
且AM=MB,AN=
ND,AR=2RE,
∴
=2
+3
+
,
∵
∥
,
∴
=kAG=k(2AM+3AN+
AR)=2kAM+3kAN+
kAR,
又∵P在平面MNR内
∴上式中AM,AN,AR前系数的和是1,
∴2k+3k+
k=1
∴k=
,
∴AP:PG=2:11.
| AM |
| AN |
| AR |

∵M、N、R分别是AB、AD、AE上的点,
且AM=MB,AN=
| 1 |
| 2 |
∴
| AG |
| AM |
| AN |
| 3 |
| 2 |
| AR |
∵
| AP |
| AG |
∴
| AP |
| 3 |
| 2 |
| 3 |
| 2 |
又∵P在平面MNR内
∴上式中AM,AN,AR前系数的和是1,
∴2k+3k+
| 3 |
| 2 |
∴k=
| 2 |
| 13 |
∴AP:PG=2:11.
点评:本题考查两线段比值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
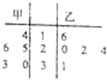 将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若
将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
用辗转相除法,计算56和264的最大公约数时,需要做的除法次数是( )
| A、3 | B、4 | C、6 | D、7 |
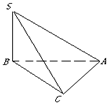 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中: