题目内容
已知函数f(x)=ax3+bx+4(a,b∈R),f(lg(log210))=5,则f[lg(lg2)]=( )
| A、-3 | B、-1 | C、3 | D、4 |
考点:函数的值
专题:函数的性质及应用
分析:令f(x)=g(x)+4,g(x)=ax3+bsinx是一个奇函数,g(lg(log210))+g(lg(lg2))=0,由此得到f(lg(lg2))=8-5=3.
解答:
解:∵函数f(x)=ax3+bx+4(a,b∈R),
lg(log210)+lg(lg2)=lg1=0,
∴lg(log210)与lg(lg2)互为相反数,
令f(x)=g(x)+4,
即g(x)=ax3+bsinx是一个奇函数,
故g(lg(log210))+g(lg(lg2))=0,
∴f(lg(log210))+f(lg(lg2))
=g(lg(log210))+4+g(lg(lg2))+4=8,
又f(lg(log210))=5,
所以f(lg(lg2))=8-5=3.
故选:C.
lg(log210)+lg(lg2)=lg1=0,
∴lg(log210)与lg(lg2)互为相反数,
令f(x)=g(x)+4,
即g(x)=ax3+bsinx是一个奇函数,
故g(lg(log210))+g(lg(lg2))=0,
∴f(lg(log210))+f(lg(lg2))
=g(lg(log210))+4+g(lg(lg2))+4=8,
又f(lg(log210))=5,
所以f(lg(lg2))=8-5=3.
故选:C.
点评:本题考查函数值的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知ξ的分布列为:
则Dξ等于( )
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示,则该几何体的表面积为( )


| A、44+π | B、40+4π |
| C、44+4π | D、44+2π |
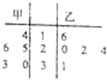 将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若
将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若(ax2+
)6的展开式中x3项的系数为20,则a2+b2的最小值为( )
| b |
| x |
| A、1 | B、2 | C、3 | D、4 |