题目内容
已知椭圆
+
=1(a>b>0)的焦距是2c,若以a,2b,c为三边长必能构成三角形,则该椭圆离心率的取值范围是 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先利用已知条件建立关系式,通过变换再利用椭圆离心率求出结果.
解答:
解:已知椭圆
+
=1(a>b>0)的焦距是2c,
则:b2=a2-c2
若以a,2b,c为三边长必能构成三角形,
则:a-c<2b<a+c
整理得:
<b<
则:(
)2<b2<(
)2
即:
解得:①式恒成立
②式解得:e>
由于椭圆离心率:0<e<1
所以:1>e>
故答案为:1>e>
| x2 |
| a2 |
| y2 |
| b2 |
则:b2=a2-c2
若以a,2b,c为三边长必能构成三角形,
则:a-c<2b<a+c
整理得:
| a-c |
| 2 |
| a+c |
| 2 |
则:(
| a-c |
| 2 |
| a+c |
| 2 |
即:
|
解得:①式恒成立
②式解得:e>
| 3 |
| 5 |
由于椭圆离心率:0<e<1
所以:1>e>
| 3 |
| 5 |
故答案为:1>e>
| 3 |
| 5 |
点评:本题考查的知识要点:椭圆的离心率的应用,三角形的三边关系的应用.属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知ξ的分布列为:
则Dξ等于( )
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
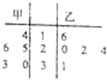 将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若
将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若(ax2+
)6的展开式中x3项的系数为20,则a2+b2的最小值为( )
| b |
| x |
| A、1 | B、2 | C、3 | D、4 |
用辗转相除法,计算56和264的最大公约数时,需要做的除法次数是( )
| A、3 | B、4 | C、6 | D、7 |
 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,求时速在[60,70]的汽车大约有多少辆?
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,求时速在[60,70]的汽车大约有多少辆?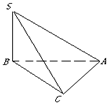 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中: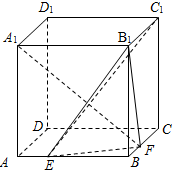 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC上的动点,且AE=BF.