题目内容
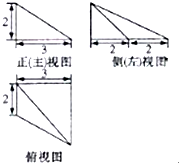
某几何体的三视图(单位:cm)如图所示,则该几何体的体积为:( )

| A、2cm2 | ||
B、
| ||
C、
| ||
| D、6cm2 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体是四棱锥P-ABCD.其中PA⊥底面ABCD,PA=2,AB=3,AD=2,BC=4,底面ABCD是直角梯形,AD∥BC,AD⊥AB.利用四棱锥的体积即可得出.
解答:
解:由三视图可知:该几何体是四棱锥P-ABCD.
其中PA⊥底面ABCD,PA=2,AB=3,AD=2,BC=4,底面ABCD是直角梯形,AD∥BC,AD⊥AB.
∴该几何体的体积V=
•PA•S梯形ABCD
=
×2×
=6.
故选:D.

其中PA⊥底面ABCD,PA=2,AB=3,AD=2,BC=4,底面ABCD是直角梯形,AD∥BC,AD⊥AB.
∴该几何体的体积V=
| 1 |
| 3 |
=
| 1 |
| 3 |
| (2+4)×3 |
| 2 |
故选:D.
点评:本题考查了四棱锥的三视图及其体积计算公式,属于基础题.

练习册系列答案
相关题目
若(ax2+
)6的展开式中x3项的系数为20,则a2+b2的最小值为( )
| b |
| x |
| A、1 | B、2 | C、3 | D、4 |
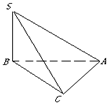 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中: