题目内容
1．数列{an}满足：an+2=an+1+an，且a1=a2=1，则a7=（ ）| A． | 7 | B． | 8 | C． | 13 | D． | 21 |
分析 利用递推关系即可得出．
解答 解：∵an+2=an+1+an，且a1=a2=1，
∴a3=a1+a2=2，同理可得：a4=3，a5=5，a6=8，a7=13．
故选：C．
点评 本题考查了数列的递推关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
习题精选系列答案
相关题目
11．
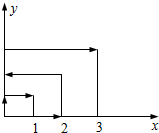如图：一个质点在第一象限运动，在第一秒钟它由原点运动到点（0，1），而后接着按图所示在与x轴y轴平行的方向运动，且每秒移动一个单位长度，那么416秒后，这个质点所处的位置的坐标是（20，16）．
如图：一个质点在第一象限运动，在第一秒钟它由原点运动到点（0，1），而后接着按图所示在与x轴y轴平行的方向运动，且每秒移动一个单位长度，那么416秒后，这个质点所处的位置的坐标是（20，16）．
6．已知点A的极坐标为（2，$\frac{3π}{4}$），则它的直角坐标是（ ）
| A． | （2，2） | B． | （1，$\frac{{\sqrt{2}}}{2}$ ） | C． | （-$\sqrt{2}$，$\sqrt{2}$） | D． | （$\sqrt{2}$，-$\sqrt{2}$） |
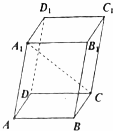如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形，AB=4，AD=3，AA1=5，∠BAA1=∠DAA1=60°，则A1C的长为$\sqrt{85}$．
10．命题“若x2＜9，则-3＜x＜3”的逆否命题是（ ）
| A． | 若x2≥9，则x≥3或x≤-3 | B． | 若-3＜x＜3，则x2＜9 | ||
| C． | 若x＞3或x＜-3，则x2＞9 | D． | 若x≥3或x≤-3，则x2≥9 |