题目内容
13.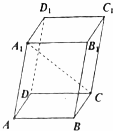 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则A1C的长为$\sqrt{85}$.
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则A1C的长为$\sqrt{85}$.
分析 根据$\overrightarrow{{A}_{1}C}$=$\overrightarrow{{A}_{1}A}$+$\overrightarrow{AB}$+$\overrightarrow{AD}$,求模长即可.
解答 解:∵$\overrightarrow{{A}_{1}C}$=$\overrightarrow{{A}_{1}A}$+$\overrightarrow{AB}$+$\overrightarrow{AD}$,
∴|$\overrightarrow{{A}_{1}C}$|2=|$\overrightarrow{{A}_{1}A}$|2+|$\overrightarrow{AB}$|2+|$\overrightarrow{AD}$|2+2$\overrightarrow{{A}_{1}A}$•$\overrightarrow{AB}$+2$\overrightarrow{{A}_{1}A}$•$\overrightarrow{AD}$+2$\overrightarrow{AB}$•$\overrightarrow{AD}$
=52+42+32+2×5×4cos60°+2×5×3cos60°+2×4×3cos90°
=85,
∴|$\overrightarrow{{A}_{1}C}$|=$\sqrt{85}$,即A1C的长是$\sqrt{85}$.
故答案为:$\sqrt{85}$.
点评 本题考查了线段长度的求法,解题时应利用空间向量的知识求模长,是基础题目.

练习册系列答案
相关题目
4.已知全集U={0,1,2,3,4,5,6,7},集合A={0,1,3,6},集合B={2,5,6,7},则(∁UB)∪A=( )
| A. | {0,1,2,3,4,5,6,7} | B. | {6} | C. | {2,4,5,6,7} | D. | {0,1,3,4,6} |
1.数列{an}满足:an+2=an+1+an,且a1=a2=1,则a7=( )
| A. | 7 | B. | 8 | C. | 13 | D. | 21 |
8.一个正方体的表面涂上红色,在它的长、宽、高上等距离地各切三刀,则大正方形被分割成若干个小正方体,从小正方体中随机的取出一个,则这个小正方体各个面都没有涂红色的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{27}$ | D. | $\frac{1}{9}$ |
18.参数方程$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$(α为参数)化成普通方程为( )
| A. | x2+(y+1)2=1 | B. | x2+(y-1)2=1 | C. | (x-1)2+(y-1)2=1 | D. | x2+y2=1 |
3.设A、B是非空数集,定义A*B={x|x∈A∪B且x∉A∩B},已知集合A={x|y=2x-x2},B={y|y=2x,x>0},则A*B=( )
| A. | [0,1]∪(2,+∞) | B. | [0,1)∪(2,+∞) | C. | (-∞,1] | D. | [0,2] |