题目内容
9.已知函数f(x)=x+$\frac{3}{x}$+2,(x≥$\sqrt{3}$).①判断函数y=f(x)在区间[$\sqrt{3}$,+∞)上的单调性,并加以证明.
②若函数g(x)=f(x)+x2-3x-$\frac{3}{x}$,且满足g(x)≥a恒成立,求a的取值范围.
分析 ①函数y=f(x)在区间[$\sqrt{3}$,+∞)上单调递增,利用导数加以证明.
②若函数g(x)=f(x)+x2-3x-$\frac{3}{x}$,且满足g(x)≥a恒成立,则x2-2x+2≥a(x≥$\sqrt{3}$)恒成立,求出左边的最小值,即可求a的取值范围.
解答 解:①函数y=f(x)在区间[$\sqrt{3}$,+∞]上单调递增.
证明如下:∵f(x)=x+$\frac{3}{x}$+2,
∴f′(x)=1-$\frac{3}{{x}^{2}}$,
∵x≥$\sqrt{3}$,
∴f′(x)=1-$\frac{3}{{x}^{2}}$≥0,
∴函数y=f(x)在区间[$\sqrt{3}$,+∞)上单调递增.
②∵函数g(x)=f(x)+x2-3x-$\frac{3}{x}$,且满足g(x)≥a恒成立,
∴x2-2x+2≥a(x≥$\sqrt{3}$)恒成立,
∵x≥$\sqrt{3}$,∴x2-2x+2≥5-2$\sqrt{3}$,
∴a≤5-2$\sqrt{3}$.
点评 本题考查函数恒成立问题,考查导数知识的运用,考查函数的单调性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.原点到直线l:x-2y+3=0的距离是( )
| A. | $\frac{\sqrt{3}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
4.已知全集U={0,1,2,3,4,5,6,7},集合A={0,1,3,6},集合B={2,5,6,7},则(∁UB)∪A=( )
| A. | {0,1,2,3,4,5,6,7} | B. | {6} | C. | {2,4,5,6,7} | D. | {0,1,3,4,6} |
1.数列{an}满足:an+2=an+1+an,且a1=a2=1,则a7=( )
| A. | 7 | B. | 8 | C. | 13 | D. | 21 |
18.参数方程$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$(α为参数)化成普通方程为( )
| A. | x2+(y+1)2=1 | B. | x2+(y-1)2=1 | C. | (x-1)2+(y-1)2=1 | D. | x2+y2=1 |
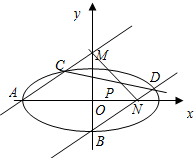 如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.
如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.