题目内容
对于平面α，β，γ和直线a，b，m，n，下列命题中真命题是（ ）
| A、若a⊥m，a⊥n，m?α，n?α，则a⊥α |
| B、若α∥β，α∩γ=a，β∩γ=b则a∥b |
| C、若a∥b，b?α，则a∥α |
| D、若a?β，b?β，a∥α，b∥α，则β∥α |
考点：空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题：开放型,空间位置关系与距离
分析：A．利用线面垂直的判定定理即可判断出；
B．利用两个平面平行的性质定理即可判断出；
C．利用线面平行的判定定理即可判断出；
D．利用面面平行的判定定理即可得出．
B．利用两个平面平行的性质定理即可判断出；
C．利用线面平行的判定定理即可判断出；
D．利用面面平行的判定定理即可得出．
解答：
解：对于A，a⊥m，a⊥n，m?α，n?α，m，n相交时，a⊥α，故不正确；
对于B，α∥β，α∩γ=a，β∩γ=b，利用面面平行的性质，可得a∥b，故正确；
对于C，a∥b，b?α，a?α时，a∥α，故不正确；
对于D，a?β，b?β，a∥α，b∥α，a，b相交时，β∥α，故不正确．
故选：B．
对于B，α∥β，α∩γ=a，β∩γ=b，利用面面平行的性质，可得a∥b，故正确；
对于C，a∥b，b?α，a?α时，a∥α，故不正确；
对于D，a?β，b?β，a∥α，b∥α，a，b相交时，β∥α，故不正确．
故选：B．
点评：本题综合考查了空间中的线面、面面平行于垂直的位置关系，属于基础题．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
一个正三棱柱的每一条棱长都是a，则经过底面一边和相对侧棱的一个端点的截面（即图中△ACD）的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
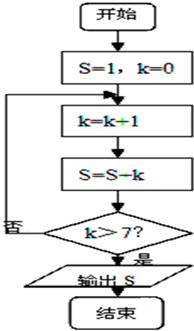执行如图所示的程序框图，则输出的结果是（ ）| A、28 | B、29 | C、36 | D、37 |
已知一元二次不等式f（x）≤0的解集为{x|x≤
，或x≥3}，则f（ex）＞0的解集为（ ）
| 1 |
| 2 |
| A、{x|x＜-ln2，或x＞ln3} |
| B、{x|ln2＜x＜ln3} |
| C、{x|x＜ln3}} |
| D、{x|-ln2＜x＜ln3} |
设l、m是两条不同的直线，α、β是两个不同的平面，则下列正确的是（ ）
| A、若l⊥α，l⊥β，则α∥β |
| B、若l∥α，α⊥β，则l⊥β |
| C、若l∥m，m∥α，则l∥α |
| D、若α⊥β，α∩β=l，l⊥m，则m⊥α |
如图，在长方体ABCD-A1B1C1D1中，AB=2，AA1=AD=1，点E、F、G分别是各自所在棱的中点．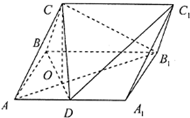
在三棱柱ABC-A1B1C1中，侧面ABBA1为矩形，AB=1，AA1=