题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,其中左焦点F(-2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线y=x+m与椭圆C交于两个不同的两点A,B,且线段的中点M总在圆x2+y2=1的内部,求实数m的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线y=x+m与椭圆C交于两个不同的两点A,B,且线段的中点M总在圆x2+y2=1的内部,求实数m的取值范围.
考点:椭圆的简单性质
专题:
分析:(Ⅰ)由椭圆C:
+
=1(a>b>0)的离心率为
,其中左焦点F(-2,0),建立方程组,求出a,b,由此能够得到椭圆C的方程.
(Ⅱ)设点A、B的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),由直线代入椭圆方程消y得,3x2+4mx+2m2-8=0,再由根的判断式结合题设条件能够得到m的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅱ)设点A、B的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),由直线代入椭圆方程消y得,3x2+4mx+2m2-8=0,再由根的判断式结合题设条件能够得到m的取值范围.
解答:
解:(Ⅰ)∵椭圆的离心率为
,其中左焦点F(-2,0).
∴
,
∴a=2
,b=2,
∴椭圆C的方程为
+
=1;
(Ⅱ)设点A、B的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由直线代入椭圆方程消y得,3x2+4mx+2m2-8=0,
△=96-8m2>0,∴-2
<m<2
.
∴x0=
=-
,y0=x0+m=
.
∵点M(x0,y0)在圆x2+y2=1上的内部,
∴(-
)2+(
)2<1,
∴-
<m<
.
| ||
| 2 |
∴
|
∴a=2
| 2 |
∴椭圆C的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(Ⅱ)设点A、B的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由直线代入椭圆方程消y得,3x2+4mx+2m2-8=0,
△=96-8m2>0,∴-2
| 3 |
| 3 |
∴x0=
| x1+x2 |
| 2 |
| 2m |
| 3 |
| m |
| 3 |
∵点M(x0,y0)在圆x2+y2=1上的内部,
∴(-
| 2m |
| 3 |
| m |
| 3 |
∴-
3
| ||
| 5 |
3
| ||
| 5 |
点评:本题考查椭圆方程的求法和直线与椭圆位置关系的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目
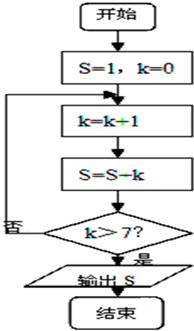 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )| A、28 | B、29 | C、36 | D、37 |
阅读如图所示的程序框图,运行相应的程序,输出的s值等于( )


| A、-3 | B、-21 | C、3 | D、21 |
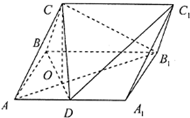 在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=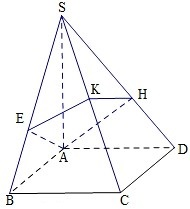 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.