题目内容
已知向量
=（1，m），
=（cosx，sinx），函数f（x）=
•
-2．
（1）设m=1，x为某三角形的内角，求f（x）=-1时x的值；
（2）设m=
，当函数f（x）取最大值时，求cos2x的值．
| a |
| b |
| a |
| b |
（1）设m=1，x为某三角形的内角，求f（x）=-1时x的值；
（2）设m=
| 3 |
考点：平面向量数量积的运算,三角函数中的恒等变换应用
专题：函数的性质及应用
分析：（1）利用两个向量的数量积公式求得当m=1时，f（x）的解析式，再由f（x）=-1时，求得sin（x+
）=
，结合x为三角形的内角，求得x的值．
（2）当m=
时，f（x）=2sin（x+
）-2，根据函数f（x）取得最大值为0，可得此时x+
=2kπ+
，k∈z，求得x的值，从而求得cos2x的值．
| π |
| 4 |
| ||
| 2 |
（2）当m=
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答：
解：（1）由题可知，函数f（x）=
•
-2=msinx+cosx-2，
当m=1时，f（x）=sinx+cosx-2=
sin（x+
）-2，
∴当f（x）=-1时，sin（x+
）=
，
∵x为三角形的内角，
∴x+
=
，
∴x=
．
（2）当m=
时，f（x）=
sinx+cosx-2=2sin（x+
）-2，
当且仅当 sin（x+
）=1时，函数f（x）取得最大值为0．
此时，x+
=2kπ+
，k∈z，
∴x=2kπ+
，k∈z，
cos2x=cos[2（2kπ+
）]=cos
=-
．
| a |
| b |
当m=1时，f（x）=sinx+cosx-2=
| 2 |
| π |
| 4 |
∴当f（x）=-1时，sin（x+
| π |
| 4 |
| ||
| 2 |
∵x为三角形的内角，
∴x+
| π |
| 4 |
| 3π |
| 4 |
∴x=
| π |
| 2 |
（2）当m=
| 3 |
| 3 |
| π |
| 6 |
当且仅当 sin（x+
| π |
| 6 |
此时，x+
| π |
| 6 |
| π |
| 2 |
∴x=2kπ+
| π |
| 3 |
cos2x=cos[2（2kπ+
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
点评：本题主要考查两个向量的数量积公式，三角函数的恒等变换，正弦函数的定义域和值域，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
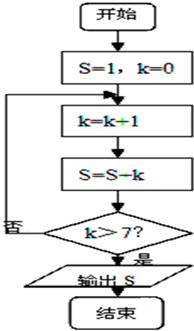执行如图所示的程序框图，则输出的结果是（ ）| A、28 | B、29 | C、36 | D、37 |
设l、m是两条不同的直线，α、β是两个不同的平面，则下列正确的是（ ）
| A、若l⊥α，l⊥β，则α∥β |
| B、若l∥α，α⊥β，则l⊥β |
| C、若l∥m，m∥α，则l∥α |
| D、若α⊥β，α∩β=l，l⊥m，则m⊥α |
如图，在长方体ABCD-A1B1C1D1中，AB=2，AA1=AD=1，点E、F、G分别是各自所在棱的中点．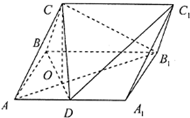
在三棱柱ABC-A1B1C1中，侧面ABBA1为矩形，AB=1，AA1=
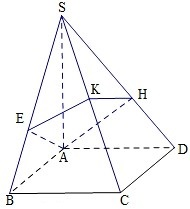如图，四棱锥S-ABCD的底面是正方形，侧棱SA⊥底面ABCD，过A作AE垂直SB交SB于E点，作AH垂直SD交SD于H点，平面AEH交SC于K点，且AB=1，SA=2．