题目内容
 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.(Ⅰ)求证:AE⊥PB;
(Ⅱ)求PB与面PAC所成角的正切值;
(Ⅲ)求异面直线PB与AC所成角的余弦值.
考点:异面直线及其所成的角,直线与平面所成的角
专题:空间角
分析:(Ⅰ)利用线面垂直的判定和性质可得BC⊥平面PAC,因此BC⊥AE.由于PA⊥⊙O所在的平面,可得∠PCA是PC与⊙O所在的平面成的角,于是∠ACP=45°.
又E是PC中点,可得AE⊥PC.得到AE⊥平面PBC,即可.
(II)由(I)可知:BC⊥面PAC,因此∠BPC即为PB与面PAC所成角.在Rt△BPC中,tan∠BPC=
即可得出.
(III)过B作AC的平行线BD交圆于D.则∠PBD为两异面直线所成的角.在△PBD中,由余弦定理可得cos∠PBD=
即可得出.
又E是PC中点,可得AE⊥PC.得到AE⊥平面PBC,即可.
(II)由(I)可知:BC⊥面PAC,因此∠BPC即为PB与面PAC所成角.在Rt△BPC中,tan∠BPC=
| BC |
| PC |
(III)过B作AC的平行线BD交圆于D.则∠PBD为两异面直线所成的角.在△PBD中,由余弦定理可得cos∠PBD=
| PB2+BD2-PD2 |
| 2PB•BD |
解答:
(Ⅰ)证明:∵PA⊥⊙O所在的平面,∴PC⊥BC,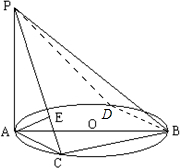
∵BC⊥AC,PA∩AC=A,
∴BC⊥平面PAC,
∴BC⊥AE.
∵PA⊥⊙O所在的平面,
∴∠PCA是PC与⊙O所在的平面成的角,
∵PC与⊙O所在的平面成45°角,
∴∠ACP=45°.
∴PA=AC.
∵E是PC中点,
∴AE⊥PC.
又PC∩BC=C,
∴AE⊥平面PBC,PB?面PBC,
∴AE⊥PB;
(Ⅱ)解:由(I)可知:BC⊥面PAC,
∴∠BPC即为PB与面PAC所成角.
在Rt△BPC中,tan∠BPC=
=
.
(Ⅲ)解:过B作AC的平行线BD交圆于D.则∠PBD为两异面直线所成的角.
由BD=
,PB=
,PD=2,
在△PBD中,由余弦定理可得cos∠PBD=
=
.

∵BC⊥AC,PA∩AC=A,
∴BC⊥平面PAC,
∴BC⊥AE.
∵PA⊥⊙O所在的平面,
∴∠PCA是PC与⊙O所在的平面成的角,
∵PC与⊙O所在的平面成45°角,
∴∠ACP=45°.
∴PA=AC.
∵E是PC中点,
∴AE⊥PC.
又PC∩BC=C,
∴AE⊥平面PBC,PB?面PBC,
∴AE⊥PB;
(Ⅱ)解:由(I)可知:BC⊥面PAC,
∴∠BPC即为PB与面PAC所成角.
在Rt△BPC中,tan∠BPC=
| BC |
| PC |
| ||
| 2 |
(Ⅲ)解:过B作AC的平行线BD交圆于D.则∠PBD为两异面直线所成的角.
由BD=
| 2 |
| 6 |
在△PBD中,由余弦定理可得cos∠PBD=
| PB2+BD2-PD2 |
| 2PB•BD |
| ||
| 3 |
点评:本题综合考查了线面垂直的判定与性质定理、线面角、异面直线所成的角、余弦定理、直角三角形的边角关系等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
将一枚骰子连续抛掷两次,则向上点数之差的绝对值不大于3的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
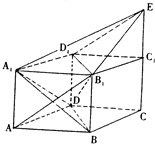 如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.
如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.