题目内容
3.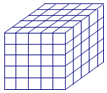 如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.
如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.
分析 由题意可知:X所有可能取值为0,1,2,3.①8个顶点处的8个小正方体涂有3面,②每一条棱上除了两个顶点处的小正方体,还剩下3个,一共有3×12=36个小正方体涂有2面,
③每个表面去掉四条棱上的16个小正方形,还剩下9个小正方形,因此一共有9×6=54个小正方体涂有一面,④由以上可知:还剩下125-(8+36+54)=27个内部的小正方体的6个面都没有涂油漆,根据上面的分析即可得出其概率及X的分布列,利用数学期望的计算公式即可得出.
解答 解:由题意可知:X所有可能取值为0,1,2,3.
①8个顶点处的8个小正方体涂有3面,∴P(X=3)=$\frac{8}{125}$,
②每一条棱上除了两个顶点处的小正方体,还剩下3个,一共有3×12=36个小正方体涂有2面,∴P(X=2)=$\frac{36}{125}$,
③每个表面去掉四条棱上的16个小正方形,还剩下9个小正方形,因此一共有9×6=54个小正方体涂有一面,∴P(X=1)=$\frac{54}{125}$,
④由以上可知:还剩下125-(8+36+54)=27个内部的小正方体的6个面都没有涂油漆,∴P(X=0)=$\frac{27}{125}$.
因此E(X)=3×$\frac{8}{125}$+2×$\frac{36}{125}$+1$\frac{54}{125}$+0×$\frac{27}{125}$=$\frac{6}{5}$.
故答案为:$\frac{6}{5}$
点评 正确找出所涂油漆的面数的正方体的个数及古典概型的概率计算公式、分布列与数学期望是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.等比数列{an}中,a2+a4=20,a3+a5=40,则a6=( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
18.已知随机变量X~B(n,$\frac{1}{3}$),若D(x)=$\frac{4}{3}$,则P(X=2)=( )
| A. | $\frac{13}{15}$ | B. | $\frac{2}{81}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
15.已知向量$\overrightarrow{OP}=(-8m,-6cos\frac{π}{3})$与单位向量(1,0)所成的角为θ,且$cosθ=-\frac{4}{5}$,则m的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
12.定义在R上的偶函数f(x)满足:对于任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)[f(x2)-f(x1)]>0,则当n∈N*时,有( )
| A. | f(-n)<f(n-1)<f(n+1) | B. | f(n-1)<f(-n)<f(n+1) | C. | f(n+1)<f(-n)<f(n-1) | D. | f(n+1)<f(n-1)<f(-n) |
3.已知集合A={x∈N*|-2<x≤2},B={y|y=2x,x∈A}|,C={z|z=1+log2y,y∈B},则A∩C=( )
| A. | {1,2} | B. | {2} | C. | {2,3,4} | D. | {1,2,3,4} |
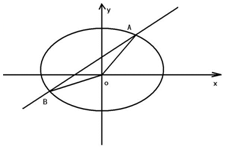 已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.
已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.