题目内容
（1）|x+2|+|x-1|＜4；
（2）|x+2|+|x-1|＞a恒成立，求a的取值范围．
（2）|x+2|+|x-1|＞a恒成立，求a的取值范围．
考点：绝对值不等式的解法
专题：综合题,不等式的解法及应用
分析：（1）分类讨论，利用不等式，即可得出结论；
（2）由绝对值不等式的性质求得|x+2|+|x-1|的最小值为3，可得a＜3，由此求得a的范围．
（2）由绝对值不等式的性质求得|x+2|+|x-1|的最小值为3，可得a＜3，由此求得a的范围．
解答：
解：（1）x＜-2时，-x-2-x+1＜4，∴x＞-2.5，∴-2.5＜x＜-2；
-2≤x≤1时，x+2-x+1＜4，∴-2≤x≤1；
x＞1时，x+2+x-1＜4，∴x＜1.5，∴1＜x＜1.5，
∴不等式的解集为{x|-2.5＜x＜1.5}；
（2）∵|x+2|+|x-1|=|x+2|+|1-x|≥|x+2+1-x|=3，
∴|x+2|+|x-1|的最小值为3，
∴a＜3，即a的范围为（-∞，3）．
-2≤x≤1时，x+2-x+1＜4，∴-2≤x≤1；
x＞1时，x+2+x-1＜4，∴x＜1.5，∴1＜x＜1.5，
∴不等式的解集为{x|-2.5＜x＜1.5}；
（2）∵|x+2|+|x-1|=|x+2|+|1-x|≥|x+2+1-x|=3，
∴|x+2|+|x-1|的最小值为3，
∴a＜3，即a的范围为（-∞，3）．
点评：本题主要考查绝对值不等式的性质，函数的恒成立问题，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
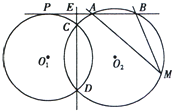已知⊙O1和⊙O2交于点C和D，⊙O1上的点P处的切线交⊙O2于A、B点，交直线CD于点E，M是⊙O2上的一点，若PE=2，EA=1，∠AMB=30°，求⊙O2的半径．
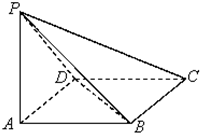如图，已知四棱锥P-ABCD，侧棱PA⊥平面ABCD，底面ABCD为菱形，∠DAB=60°且PA=AB，则直线AB与平面PBC所成角的正弦值为