题目内容
某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定,他们三人都有“同意”、“中立”、“反对”三类票各一张,投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为
,他们的投票相互没有影响,规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目的投资.
(1)求该公司决定对该项目投资的概率;
(2)求该公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率.
| 1 |
| 3 |
(1)求该公司决定对该项目投资的概率;
(2)求该公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率.
考点:古典概型及其概率计算公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)利用n次独立重复试验中事件A恰有k次发生的概率计算公式能求出该公司决定对该项目投资的概率.
(2)该公司放弃对该项目投资且投票结果中最多有一张“中立”票,有四种情形,分类进行讨论能求出结果.
(2)该公司放弃对该项目投资且投票结果中最多有一张“中立”票,有四种情形,分类进行讨论能求出结果.
解答:
解:(1)该公司决定对该项目投资的概率为P=
(
)2(
)+
(
)3=
.
(2)该公司放弃对该项目投资且投票结果中最多有一张“中立”票,
有以下四种情形:
P(A)=(
)3=
,P(B)=
(
)3=
,
P(C)=
(
)3=
,P(D)=
(
)3=
,
∵A、B、C、D互斥,
∴P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)=
.
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 3 3 |
| 1 |
| 3 |
| 7 |
| 27 |
(2)该公司放弃对该项目投资且投票结果中最多有一张“中立”票,
有以下四种情形:
| “同意”票张数 | “中立”票张数 | “反对”票张数 | |
| 事件A | 0 | 0 | 3 |
| 事件B | 1 | 0 | 2 |
| 事件C | 1 | 1 | 1 |
| 事件D | 0 | 1 | 2 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 9 |
P(C)=
| C | 1 3 |
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 9 |
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 9 |
∵A、B、C、D互斥,
∴P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)=
| 13 |
| 27 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰有k次发生的概率计算公式的灵活运用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
在△ABC中,∠C=90°,BC=2,AC=4,AB边上点P到边AC、BC的距离乘积的取值范围是( )
| A、[0,2] | ||
| B、[0,3] | ||
| C、[0,4] | ||
D、[0,
|

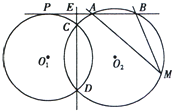 已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.
已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.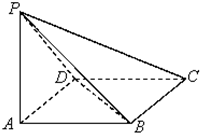 如图,已知四棱锥P-ABCD,侧棱PA⊥平面ABCD,底面ABCD为菱形,∠DAB=60°且PA=AB,则直线AB与平面PBC所成角的正弦值为
如图,已知四棱锥P-ABCD,侧棱PA⊥平面ABCD,底面ABCD为菱形,∠DAB=60°且PA=AB,则直线AB与平面PBC所成角的正弦值为