题目内容
 如图所示,已知正四棱柱ABCD-A1B1C1D1中,底面边长为2
如图所示,已知正四棱柱ABCD-A1B1C1D1中,底面边长为2| 2 |
(1)求异面直线D1E和DC所成角的正切值;
(2)求证:平面B1EF⊥平面BDD1B1.
考点:平面与平面垂直的判定,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)在正四棱柱中,异面直线D1E和DC所成的角,即D1E和AB所成的角,然后通过解直角三角形求解;
(2)证平面B1EF⊥平面BDD1B1,只需证明EF垂直于平面BDD1B1,由正四棱柱的性质即可证明.
(2)证平面B1EF⊥平面BDD1B1,只需证明EF垂直于平面BDD1B1,由正四棱柱的性质即可证明.
解答:
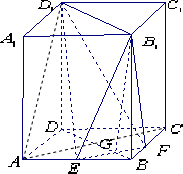 证明:(Ⅰ)连结AD1.
证明:(Ⅰ)连结AD1.
∵ABCD-A1B1C1D1 是正四棱柱,
∴AA1⊥平面ABCD.
∴平面ADD1A1⊥平面ABCD.
又AB⊥AD,
∴AB⊥平面ADD1A1.
∴AB⊥AD1.
由已知AD=2
,DD1=4,
∴AD1=
=2
.
而AE=
,
∴tan∠ADE1=
=2
.
∵CD∥AB.
∴DC与D1E所成的角就是AB与D1E所成的角,即∠D1EA.
∴直线DC与D1E所成的角为arctan2
;
(Ⅱ)连结AC,由已知,EF∥AC,AC⊥BD.
∴EF⊥BD.
又BB1⊥EF,且BD∩B1B=B.
∴EF⊥平面BDD1B1.
∵EF?平面EFB1.
∴平面B1EF⊥平面BDD1B1.
 证明:(Ⅰ)连结AD1.
证明:(Ⅰ)连结AD1.∵ABCD-A1B1C1D1 是正四棱柱,
∴AA1⊥平面ABCD.
∴平面ADD1A1⊥平面ABCD.
又AB⊥AD,
∴AB⊥平面ADD1A1.
∴AB⊥AD1.
由已知AD=2
| 2 |
∴AD1=
| AD2+DD12 |
| 6 |
而AE=
| 2 |
∴tan∠ADE1=
| AD1 |
| AE |
| 3 |
∵CD∥AB.
∴DC与D1E所成的角就是AB与D1E所成的角,即∠D1EA.
∴直线DC与D1E所成的角为arctan2
| 3 |
(Ⅱ)连结AC,由已知,EF∥AC,AC⊥BD.
∴EF⊥BD.
又BB1⊥EF,且BD∩B1B=B.
∴EF⊥平面BDD1B1.
∵EF?平面EFB1.
∴平面B1EF⊥平面BDD1B1.
点评:本题考查了异面直线所成的角,考查了面与面的垂直,综合考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目

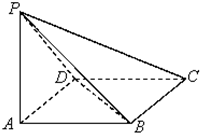 如图,已知四棱锥P-ABCD,侧棱PA⊥平面ABCD,底面ABCD为菱形,∠DAB=60°且PA=AB,则直线AB与平面PBC所成角的正弦值为
如图,已知四棱锥P-ABCD,侧棱PA⊥平面ABCD,底面ABCD为菱形,∠DAB=60°且PA=AB,则直线AB与平面PBC所成角的正弦值为