题目内容
已知f(x)=x2+a|x-1|+1,若f(x)≥0恒成立,求a的范围.
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:f(x)≥0恒成立,即x2+a|x-1|+1≥0恒成立,分类讨论,分离参数,利用基本不等式,即可求a的范围.
解答:
解:f(x)≥0恒成立,即x2+a|x-1|+1≥0恒成立,
若x=1,x2+1≥0恒成立;
若x>1,a≥
,令1-x=t(t<0),则
=t+
-2≤-2
-2(t=-
时取等号),∴a≥-2
-2;
若x<1时,a≥
,令x-1=t(t<0),则
=t+
+2≤-2
+2(t=-
时取等号),∴a≥-2
+2,
综上,a≥-2
+2.
若x=1,x2+1≥0恒成立;
若x>1,a≥
| x2+1 |
| 1-x |
| x2+1 |
| 1-x |
| 2 |
| t |
| 2 |
| 2 |
| 2 |
若x<1时,a≥
| x2+1 |
| x-1 |
| x2+1 |
| x-1 |
| 2 |
| t |
| 2 |
| 2 |
| 2 |
综上,a≥-2
| 2 |
点评:本题考查恒成立问题,考查基本不等式的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
设双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F且垂直于l1的直线分别交l1,l2于A,B两点,已知
与
同向,且丨
丨是丨
丨,丨
丨的等差中项,则l1,l2的方程是( )
| BF |
| FA |
| AB |
| OA |
| OB |
A、y=±
| ||
| B、y=±2x | ||
C、y=±
| ||
D、y=±
|
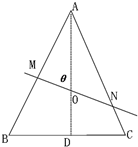 如图,等边△ABC中,AB=3,O为中心,过O的直线交AB于M,交AC于N,设∠AOM=θ(0≤θ≤120°),当θ分别为何值时,
如图,等边△ABC中,AB=3,O为中心,过O的直线交AB于M,交AC于N,设∠AOM=θ(0≤θ≤120°),当θ分别为何值时,