ΧβΡΩΡΎ»ί
 Ρ≥Ά§―ß”ΟΓΕΦΗΚΈΜ≠ΑεΓΖ―–ΨΩ≈ΉΈοœΏΒΡ–‘÷ ΘΚ¥ρΩΣΓΕΦΗΚΈΜ≠ΑεΓΖ»μΦΰΘ§Μφ÷ΤΡ≥≈ΉΈοœΏEΘΚy2=2pxΘ§‘Ύ≈ΉΈοœΏ…œ»Έ“βΜ≠“ΜΗωΒψSΘ§Ε»ΝΩΒψSΒΡΉχ±ξΘ®xSΘ§ySΘ©Θ§»γΆΦΘ°
Ρ≥Ά§―ß”ΟΓΕΦΗΚΈΜ≠ΑεΓΖ―–ΨΩ≈ΉΈοœΏΒΡ–‘÷ ΘΚ¥ρΩΣΓΕΦΗΚΈΜ≠ΑεΓΖ»μΦΰΘ§Μφ÷ΤΡ≥≈ΉΈοœΏEΘΚy2=2pxΘ§‘Ύ≈ΉΈοœΏ…œ»Έ“βΜ≠“ΜΗωΒψSΘ§Ε»ΝΩΒψSΒΡΉχ±ξΘ®xSΘ§ySΘ©Θ§»γΆΦΘ°Θ®ΔώΘ©ΆœΕ·ΒψSΘ§ΖΔœ÷Β±xS=4 ±Θ§yS=4Θ§ ‘«σ≈ΉΈοœΏEΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©…η≈ΉΈοœΏEΒΡΕΞΒψΈΣAΘ§ΫΙΒψΈΣFΘ§ΙΙ‘λ÷±œΏSFΫΜ≈ΉΈοœΏE”Ύ≤ΜΆ§ΝΫΒψSΓΔTΘ§ΙΙ‘λ÷±œΏASΓΔATΖ÷±πΫΜΉΦœΏ”ΎMΓΔNΝΫΒψΘ§ΙΙ‘λ÷±œΏMTΓΔNSΘ°Ψ≠Ιέ≤λΒΟΘΚ―ΊΉ≈≈ΉΈοœΏEΘ§Έό¬έ‘θ―υΆœΕ·ΒψSΘ§Κψ”–MTΓΈNSΘ°«κΡψ÷ΛΟς’β“ΜΫα¬έΘ°
Θ®ΔσΘ©ΈΣΫχ“Μ≤Ϋ―–ΨΩΗΟ≈ΉΈοœΏEΒΡ–‘÷ Θ§Ρ≥Ά§―ßΫχ––ΝΥœ¬ΟφΒΡ≥Δ ‘ΘΚ‘ΎΘ®ΔρΘ©÷–Θ§Α―ΓΑΫΙΒψFΓ±ΗΡ±δΈΣΤδΥϋΓΑΕ®ΒψGΘ®gΘ§0Θ©Θ®gΓΌ0Θ©Γ±Θ§Τδ”ύΧθΦΰ≤Μ±δΘ§ΖΔœ÷ΓΑMT”κNS≤Μ‘ΌΤΫ––Γ±Θ° «ΖώΩ…“‘ Β±ΗϋΗΡΘ®ΔρΘ©÷–ΒΡΤδΥϋΧθΦΰΘ§ ΙΒΟ»‘”–ΓΑMTΓΈNSΓ±≥…ΝΔΘΩ»γΙϊΩ…“‘Θ§«κ–¥≥ωœύ”ΠΒΡ’ΐ»ΖΟϋΧβΘΜΖώ‘ρΘ§ΥΒΟςάμ”…Θ°
ΩΦΒψΘΚ÷±œΏ”κ‘≤ΉΕ«ζœΏΒΡΉέΚœΈ Χβ
Ή®ΧβΘΚΉέΚœΧβ,‘≤ΉΕ«ζœΏΒΡΕ®“εΓΔ–‘÷ ”κΖΫ≥Χ
Ζ÷ΈωΘΚΘ®ΔώΘ©Α―xS=4Θ§yS=4¥ζ»κy2=2pxΘ§ΒΟpΘ§Φ¥Ω…«σ≥ω≈ΉΈοœΏEΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©…η÷±œΏlΘΚmy=x-1Θ§¥ζ»κ≈ΉΈοœΏΖΫ≥ΧΘ§«σ≥ωMΘ§NΒΡΉχ±ξΘ§Ω…ΒΟ
ΓΔ
ΒΡΉχ±ξΘ§÷ΛΟς
ΓΈ
Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®ΔσΘ©…η≈ΉΈοœΏEΘΚy2=4xΒΡΕΞΒψΈΣAΘ§Ε®ΒψGΘ®gΘ§0Θ©Θ®gΓΌ0Θ©Θ§ΙΐΒψGΒΡ÷±œΏl”κ≈ΉΈοœΏEœύΫΜ”ΎSΓΔTΝΫΒψΘ§÷±œΏASΓΔATΖ÷±πΫΜ÷±œΏx=-g”ΎMΓΔNΝΫΒψΘ§‘ρMTΓΈNSΘ°
Θ®ΔρΘ©…η÷±œΏlΘΚmy=x-1Θ§¥ζ»κ≈ΉΈοœΏΖΫ≥ΧΘ§«σ≥ωMΘ§NΒΡΉχ±ξΘ§Ω…ΒΟ
| MT |
| NS |
| MT |
| NS |
Θ®ΔσΘ©…η≈ΉΈοœΏEΘΚy2=4xΒΡΕΞΒψΈΣAΘ§Ε®ΒψGΘ®gΘ§0Θ©Θ®gΓΌ0Θ©Θ§ΙΐΒψGΒΡ÷±œΏl”κ≈ΉΈοœΏEœύΫΜ”ΎSΓΔTΝΫΒψΘ§÷±œΏASΓΔATΖ÷±πΫΜ÷±œΏx=-g”ΎMΓΔNΝΫΒψΘ§‘ρMTΓΈNSΘ°
Ϋβ¥πΘΚ
ΫβΘΚΘ®ΔώΘ©Α―xS=4Θ§yS=4¥ζ»κy2=2pxΘ§ΒΟp=2Θ§Γ≠Θ®3Ζ÷Θ©
“ρ¥ΥΘ§≈ΉΈοœΏEΒΡΖΫ≥Χy2=4xΘ°Γ≠Θ®4Ζ÷Θ©
Θ®ΔρΘ©“ρΈΣ≈ΉΈοœΏEΒΡΫΙΒψΈΣFΘ®1Θ§0Θ©Θ§…ηSΘ®x1Θ§y1Θ©Θ§TΘ®x2Θ§y2Θ©Θ§
“άΧβ“βΩ……η÷±œΏlΘΚmy=x-1Θ§
¥ζ»κ≈ΉΈοœΏΖΫ≥ΧΒΟy2-4my-4=0Θ§
‘ρy1+y2=4mΘ§y1y2=-4 ΔΌΓ≠Θ®6Ζ÷Θ©
”÷“ρΈΣlASΘΚy=
•xΘ§lATΘΚy=
•xΘ§
Υυ“‘MΘ®-1Θ§-
Θ©Θ§NΘ®-1Θ§-
Θ©Θ§
Υυ“‘
=Θ®x2+1Θ§y2+
Θ©Θ§
=Θ®x1+1Θ§y1+
Θ©Θ§Γ≠Θ®7Ζ÷Θ©
”÷“ρΈΣΘ®y2+
Θ©Θ®x1+1Θ©-Θ®y1+
Θ©Θ®x2+1Θ©Θ§Γ≠Θ®8Ζ÷Θ©
=Θ®y1-y2Θ©Θ®
Θ©Θ§ΔΎ
Α―ΔΌ¥ζ»κΔΎΘ§ΒΟΘ®y1-y2Θ©Θ®
Θ©=0Θ§Γ≠Θ®10Ζ÷Θ©
Φ¥Θ®y2+
Θ©Θ®x1+1Θ©-Θ®y1+
Θ©Θ®x2+1Θ©=0Θ§
Υυ“‘
ΓΈ
Θ§
”÷“ρΈΣMΓΔTΓΔNΓΔSΥΡΒψ≤ΜΙ≤œΏΘ§Υυ“‘MTΓΈNSΘ°Γ≠Θ®11Ζ÷Θ©
Θ®ΔσΘ©…η≈ΉΈοœΏEΘΚy2=4xΒΡΕΞΒψΈΣAΘ§Ε®ΒψGΘ®gΘ§0Θ©Θ®gΓΌ0Θ©Θ§ΙΐΒψGΒΡ÷±œΏl”κ≈ΉΈοœΏEœύΫΜ”ΎSΓΔTΝΫΒψΘ§÷±œΏASΓΔATΖ÷±πΫΜ÷±œΏx=-g”ΎMΓΔNΝΫΒψΘ§‘ρMTΓΈNSΘ°Γ≠Θ®14Ζ÷Θ©
“ρ¥ΥΘ§≈ΉΈοœΏEΒΡΖΫ≥Χy2=4xΘ°Γ≠Θ®4Ζ÷Θ©
Θ®ΔρΘ©“ρΈΣ≈ΉΈοœΏEΒΡΫΙΒψΈΣFΘ®1Θ§0Θ©Θ§…ηSΘ®x1Θ§y1Θ©Θ§TΘ®x2Θ§y2Θ©Θ§
“άΧβ“βΩ……η÷±œΏlΘΚmy=x-1Θ§
¥ζ»κ≈ΉΈοœΏΖΫ≥ΧΒΟy2-4my-4=0Θ§
‘ρy1+y2=4mΘ§y1y2=-4 ΔΌΓ≠Θ®6Ζ÷Θ©
”÷“ρΈΣlASΘΚy=
| y1 |
| x1 |
| y2 |
| x2 |
Υυ“‘MΘ®-1Θ§-
| y1 |
| x1 |
| y2 |
| x2 |
Υυ“‘
| MT |
| y1 |
| x1 |
| NS |
| y2 |
| x2 |
”÷“ρΈΣΘ®y2+
| y1 |
| x1 |
| y2 |
| x2 |
=Θ®y1-y2Θ©Θ®
| y12y22-16 |
| 4y1y2 |
Α―ΔΌ¥ζ»κΔΎΘ§ΒΟΘ®y1-y2Θ©Θ®
| y12y22-16 |
| 4y1y2 |
Φ¥Θ®y2+
| y1 |
| x1 |
| y2 |
| x2 |
Υυ“‘
| MT |
| NS |
”÷“ρΈΣMΓΔTΓΔNΓΔSΥΡΒψ≤ΜΙ≤œΏΘ§Υυ“‘MTΓΈNSΘ°Γ≠Θ®11Ζ÷Θ©
Θ®ΔσΘ©…η≈ΉΈοœΏEΘΚy2=4xΒΡΕΞΒψΈΣAΘ§Ε®ΒψGΘ®gΘ§0Θ©Θ®gΓΌ0Θ©Θ§ΙΐΒψGΒΡ÷±œΏl”κ≈ΉΈοœΏEœύΫΜ”ΎSΓΔTΝΫΒψΘ§÷±œΏASΓΔATΖ÷±πΫΜ÷±œΏx=-g”ΎMΓΔNΝΫΒψΘ§‘ρMTΓΈNSΘ°Γ≠Θ®14Ζ÷Θ©
ΒψΤάΘΚ±Ψ–ΓΧβ÷ς“ΣΩΦ≤ι≈ΉΈοœΏΒΡ±ξΉΦΖΫ≥ΧΓΔ÷±œΏ”κ‘≤ΉΕ«ζœΏΒΡΈΜ÷ΟΙΊœΒΒ»Μυ¥Γ÷Σ ΕΘ§ΩΦ≤ιΆΤάμ¬έ÷ΛΡήΝΠΓΔ‘ΥΥψ«σΫβΡήΝΠΘ§ΩΦ≤ιΜ·Ιι”κΉΣΜ·ΥΦœκΓΔΖ÷άύ”κ’ϊΚœΥΦœκΓΔ ΐ–ΈΫαΚœΥΦœκΒ»Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
»γΙϊxΘΨyΘΨ0Θ§‘ρ
=Θ®ΓΓΓΓΘ©
| xyyx |
| xxyy |
AΓΔ(x-y)
| ||
BΓΔ(x-y)
| ||
CΓΔ(
| ||
DΓΔ(
|
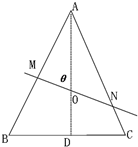 »γΆΦΘ§Β»±ΏΓςABC÷–Θ§AB=3Θ§OΈΣ÷––ΡΘ§ΙΐOΒΡ÷±œΏΫΜAB”ΎMΘ§ΫΜAC”ΎNΘ§…ηΓœAOM=Π»Θ®0ΓήΠ»Γή120ΓψΘ©Θ§Β±Π»Ζ÷±πΈΣΚΈ÷Β ±Θ§
»γΆΦΘ§Β»±ΏΓςABC÷–Θ§AB=3Θ§OΈΣ÷––ΡΘ§ΙΐOΒΡ÷±œΏΫΜAB”ΎMΘ§ΫΜAC”ΎNΘ§…ηΓœAOM=Π»Θ®0ΓήΠ»Γή120ΓψΘ©Θ§Β±Π»Ζ÷±πΈΣΚΈ÷Β ±Θ§