题目内容
9.设Sn为数列{an}的前n项和,且满足${S_n}={({-1})^n}{a_n}-\frac{1}{2^n}$,则a2=$\frac{1}{4}$;S1+S3+S5+…+S2017=$\frac{1}{3}(\frac{1}{{2}^{2018}}-1)$.分析 由${S_n}={({-1})^n}{a_n}-\frac{1}{2^n}$,当n=1时,可得a1=-a1-$\frac{1}{2}$,可得a1=-$\frac{1}{4}$.当n≥2时,an=Sn-Sn-1=(-1)nan-$\frac{1}{{2}^{n}}$-(-1)n-1an-1+$\frac{1}{{2}^{n-1}}$,a3=-a3-$\frac{1}{8}$+a2+$\frac{1}{4}$.若n为偶数,则an-1=-$\frac{1}{{2}^{n}}$,因此n为正奇数,an=-$\frac{1}{{2}^{n+1}}$,可得a3=-$\frac{1}{16}$,a2.n=2k-1(k∈N*),Sn=S2k-1=-an-$\frac{1}{{2}^{n}}$.可得S1+S3+S5+…+S2017=-(a1+a3+…+a2017)-$(\frac{1}{2}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{2017}})$,代入利用等比数列的求和公式即可得出.
解答 解:由${S_n}={({-1})^n}{a_n}-\frac{1}{2^n}$,当n=1时,可得a1=-a1-$\frac{1}{2}$,可得a1=-$\frac{1}{4}$.
当n≥2时,an=Sn-Sn-1=(-1)nan-$\frac{1}{{2}^{n}}$-(-1)n-1an-1+$\frac{1}{{2}^{n-1}}$,a3=-a3-$\frac{1}{8}$+a2+$\frac{1}{4}$.
若n为偶数,则an-1=-$\frac{1}{{2}^{n}}$,因此n为正奇数,an=-$\frac{1}{{2}^{n+1}}$,可得a3=-$\frac{1}{16}$,a2=$\frac{1}{4}$.
n=2k-1(k∈N*),Sn=S2k-1=-an-$\frac{1}{{2}^{n}}$,
∴S1+S3+S5+…+S2017=-(a1+a3+…+a2017)-$(\frac{1}{2}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{2017}})$
=$(\frac{1}{{2}^{2}}+\frac{1}{{2}^{4}}+…+\frac{1}{{2}^{2018}})$-$(\frac{1}{2}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{2017}})$
=$\frac{\frac{1}{4}(1-\frac{1}{{4}^{1009}})}{1-\frac{1}{4}}$-$\frac{\frac{1}{2}(1-\frac{1}{{4}^{1009}})}{1-\frac{1}{4}}$
=$\frac{1}{3}(\frac{1}{{2}^{2018}}-1)$.
故答案为:$\frac{1}{4},\frac{1}{3}({\frac{1}{{{2^{2018}}}}-1})$.
点评 本题考查了等比数列通项公式与求和公式、数列递推关系,考查了分类讨论方法、推理能力与计算能力,属于难题.

 天天练口算系列答案
天天练口算系列答案
| A. | i>3? | B. | i<4? | C. | i>4? | D. | i<5? |
| A. | 2x+y-2=0 | B. | 2x-y-2=0 | C. | x+y-2=0 | D. | y=0 |
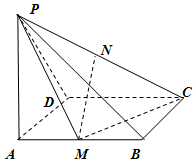 如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.
如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.(1)求证:MN∥平面PAD;
(2)求证:MN⊥平面PCD;
(3)若PA=2,AB=4,求三棱锥B-PMC的体积.
| A. | $\frac{1}{8}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{8}{15}$ |