题目内容

1．设数列{an}中a2+a4=8，点Pn（n，an）对任意的n∈N*都满足$\overrightarrow{{P_n}{P_{n+1}}}=（1，2）$，则数列{an}的前n项和Sn=n2-n．

分析 点Pn（n，an）对任意的n∈N*都满足$\overrightarrow{{P_n}{P_{n+1}}}=（1，2）$，可得an+1-an=2．利用等差数列的通项公式与求和公式即可得出．

解答 解：∵点Pn（n，an）对任意的n∈N*都满足$\overrightarrow{{P_n}{P_{n+1}}}=（1，2）$，
∴an+1-an=2．
∴数列{an}是公差为2的等差数列，
∵a2+a4=8，∴2a1+4×2=8，解得a1=0．
∴Sn=0+$\frac{n（n-1）}{2}×2$=n2-n．
故答案为：n2-n．

点评 本题考查了等差数列的定义通项公式与求和公式、平面向量坐标运算性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
11．计算：
（1）${（{\frac{16}{81}}）^{-\frac{3}{4}}}+{log_3}\frac{5}{4}+{log_3}\frac{4}{5}$
（2）log2.56.25+lg0.001+ln$\sqrt{e}+{2^{-1+{{log}_2}3}}$．
12．设定义在R上的连续函数f（x）满足：
（1）对任意的实数x，都有f（-x）-f（x）=0；
（2）对任意的实数x，都有f（x+π）+f（x）=1；
（3）当x∈[0，π]时，0≤f（x）≤1；
（4）当x∈（0，$\frac{π}{2}$）∪（$\frac{π}{2}$，π）时，有（x-$\frac{π}{2}$）f′（x）＞0（其中f′（x）为函数f（x）的导函数）．
则方程f（x）=|sinx|在[-2π，2π]上的根的个数为（　　）
A．4B．6C．8D．10
9．设Sn为数列{an}的前n项和，且满足${S_n}={（{-1}）^n}{a_n}-\frac{1}{2^n}$，则a2=$\frac{1}{4}$；S1+S3+S5+…+S2017=$\frac{1}{3}（\frac{1}{{2}^{2018}}-1）$．
16．已知a＞0且b＞0，函数g（x）=2x，且g（a）•g（b）=2，则ab的最大值是$\frac{1}{4}$．
6．半径为1的球的表面积是4π．
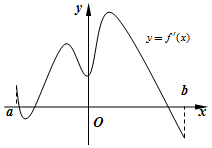13．函数f（x）的定义域为开区间（a，b），其导函数f'（x）在（a，b）图象如图所示，则函数f（x）在开区间（a，b）内的极小值的个数是1个．
10．已知函数f（x）=$\frac{1}{2}m{（x-1）^2}$-2x+3+lnx，m∈R
（1）当m=0时，求函数f（x）的单调增区间；
（2）若曲线y=f（x）在点P（1，1）处的切线l与曲线y=f（x）有且只有一个公共点，求实数m的取值范围．
11．放射性元素一般都有一个半衰期（剩留量为最初质量的一半所需的时间）．已知一种放射性元素的质量按每年10%衰减，那么这种放射性元素的半衰期是（　　）年（精确到0.1，已知lg2=0.3010，lg3=0.4771）．
A．5.2B．6.6C．7.1D．8.3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网