题目内容

4．已知函数f（x）=2（x-$\frac{1}{x}$）-2ln x，则曲线y=f（x）在点（1，f（1））处的切线方程是（　　）
A．2x+y-2=0B．2x-y-2=0C．x+y-2=0D．y=0

分析 求出原函数的导函数，求出切点坐标，切线的斜率，然后由直线方程的点斜式得曲线y=f（x）在点（1，f（1））处的切线方程．

解答 解：由函数f（x）=2（x-$\frac{1}{x}$）-2ln x，f（1）=0．
得y′=2+$\frac{2}{{x}^{2}}$-$\frac{2}{x}$，
∴y′|x=1=2．即曲线f（x）=2（x-$\frac{1}{x}$）-2ln 在点（1，0）处的切线的斜率为：2．
∴曲线f（x）=2（x-$\frac{1}{x}$）-2ln 在点（1，0）处的切线方程为y-0=2×（x-1），
整理得：2x-y-2=0．
故选：B．

点评 本题考查利用导数研究曲线上某点处的切线方程，曲线上过某点处的切线的斜率，就是函数在该点处的导数值，是中档题．

练习册系列答案
相关题目
14．已知i是虚数单位，则复数z=$\frac{4+3i}{3-4i}$的共轭复数的虚部是（　　）
A．-iB．iC．1D．-1
15．已知数列{an}的前n项和S${\;}_{n}=A{q}^{n}+B（q≠0）$，则“A=-B“是“数列{an}是等比数列”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
12．设定义在R上的连续函数f（x）满足：
（1）对任意的实数x，都有f（-x）-f（x）=0；
（2）对任意的实数x，都有f（x+π）+f（x）=1；
（3）当x∈[0，π]时，0≤f（x）≤1；
（4）当x∈（0，$\frac{π}{2}$）∪（$\frac{π}{2}$，π）时，有（x-$\frac{π}{2}$）f′（x）＞0（其中f′（x）为函数f（x）的导函数）．
则方程f（x）=|sinx|在[-2π，2π]上的根的个数为（　　）
A．4B．6C．8D．10
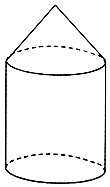19．如图，某粮仓是由圆柱和圆锥构成（粮仓的底部位于地面上），圆柱的底面直径与高都等于h米，圆锥的高为$\frac{1}{2}$h米．
（1）求这个粮仓的容积；
（2）求制作这样一个粮仓的用料面积．
9．设Sn为数列{an}的前n项和，且满足${S_n}={（{-1}）^n}{a_n}-\frac{1}{2^n}$，则a2=$\frac{1}{4}$；S1+S3+S5+…+S2017=$\frac{1}{3}（\frac{1}{{2}^{2018}}-1）$．
16．已知a＞0且b＞0，函数g（x）=2x，且g（a）•g（b）=2，则ab的最大值是$\frac{1}{4}$．
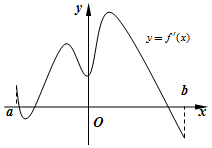13．函数f（x）的定义域为开区间（a，b），其导函数f'（x）在（a，b）图象如图所示，则函数f（x）在开区间（a，b）内的极小值的个数是1个．
14．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1（a＞0）的离心率为2，则a等于（　　）
A．2B．$\sqrt{3}$C．$\frac{3}{2}$D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网