题目内容
已知空间向量
=（2，-y，2），
=（4，2，x），|
|2+|
|2=44，且
⊥
，x，y∈R，求x，y的值．
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意可得
2+
2=x2+y2+28=44，求得x2+y2 的值．再根据
•
=x-y+4=0，联立两方程，求得x，y的值．
| a |
| b |
| a |
| b |
解答：
解：由题意可得，
2=y2+8，
2=x2+20，∴
2+
2=x2+y2+28=44，
求得x2+y2=16．
再由
⊥
，可得
•
=x-y+4=0，
又联立两方程解得：
，或
．
| a |
| b |
| a |
| b |
求得x2+y2=16．
再由
| a |
| b |
| a |
| b |
又联立两方程解得：
|
|
点评：本题主要考查两个向量的数量积公式，两个向量垂直的性质，两个向量坐标形式的运算，属于基础题．
练习册系列答案
相关题目
下列命题错误的是（ ）
A、若
| ||||||||
B、若
| ||||||||
C、当m∈R时，恒有m（
| ||||||||
D、|
|
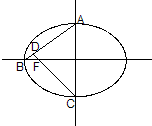已知如图，椭圆的离心率为| 1 |
| 2 |
A、-3
| ||
B、3-
| ||
C、3
| ||
D、3+
|