题目内容
设m,n是空间两条直线,α,β是空间两个平面,有下列四个命题:
①当m?α时,“n∥α”是“m∥n”的必要不充分条件;
②当m?α时,“m⊥β”是“α⊥β”的充分不必要条件;
③当n⊥α时,“n⊥β”是“α∥β”成立的充要条件;
④当m?α时,“n⊥α”是“m⊥n”的充分不必要条件;
以上四个命题正确的是 .
①当m?α时,“n∥α”是“m∥n”的必要不充分条件;
②当m?α时,“m⊥β”是“α⊥β”的充分不必要条件;
③当n⊥α时,“n⊥β”是“α∥β”成立的充要条件;
④当m?α时,“n⊥α”是“m⊥n”的充分不必要条件;
以上四个命题正确的是
考点:必要条件、充分条件与充要条件的判断
专题:空间位置关系与距离,简易逻辑
分析:根据直线与平面的平行,垂直的判断性质,结合充分必要条件的定义判断,注意举反例判断容易些.
解答:
解:∵①当m?α时,“n∥α”是“m∥n”的必要不充分条件,
n直线的位置不确定,∴①不正确,
∵②当m?α时,“m⊥β”是“α⊥β”的充分不必要条件;
根据面面垂直的判断定理可得充分条件正确,反之有可能m∥β,
∴②正确,
③当n⊥α时,“n⊥β”是“α∥β”成立的充要条件;
根据线面垂直的性质,面面平行,垂直的关系可判断③正确,
④当m?α时,“n⊥α”是“m⊥n”的充分不必要条件;
根据直线与平面垂直的定义可判断若“n⊥α”则“m⊥n”成立.
反之有可能n∥α,
故④正确
故答案为:②③④
n直线的位置不确定,∴①不正确,
∵②当m?α时,“m⊥β”是“α⊥β”的充分不必要条件;
根据面面垂直的判断定理可得充分条件正确,反之有可能m∥β,
∴②正确,
③当n⊥α时,“n⊥β”是“α∥β”成立的充要条件;
根据线面垂直的性质,面面平行,垂直的关系可判断③正确,
④当m?α时,“n⊥α”是“m⊥n”的充分不必要条件;
根据直线与平面垂直的定义可判断若“n⊥α”则“m⊥n”成立.
反之有可能n∥α,
故④正确
故答案为:②③④
点评:本题考查了空间直线与平面的平行垂直的定义,判断,性质,综合判断直线平面的位置关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在同一平面直角坐标系中,函数f(x)=lg(x+1)的图象与函数g(x)=lg(-x+1)的图象关于( )
| A、原点对称 | B、x轴对称 |
| C、直线y=x对称 | D、y轴对称 |
在△ABC中,角A、B、C所对的边分别为a、b、c.若acosA=bsinB,则,sinAcosA+cos2A=( )
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
下列函数中,既是奇函数,又是定义域上单调递减的函数为( )
| A、y=x-2 | ||
| B、y=x-1 | ||
C、y=lg
| ||
| D、y=x2 |
已知实数x、y满足
,则z=
+
的最小值为( )
|
| 9y-18 |
| x-2 |
| x-2 |
| y-2 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
下列函数与y=|x|表示同一个函数的是( )
A、y=(
| ||||||
B、y=(
| ||||||
C、y=(
| ||||||
D、y=
|
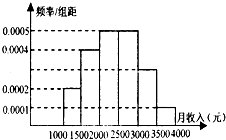 为征求个人所得税法修改建议,某机构对当地居民的月收入调查10000人,根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),因操作人员不慎,未标出第五组顶部对应的纵轴数据.
为征求个人所得税法修改建议,某机构对当地居民的月收入调查10000人,根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),因操作人员不慎,未标出第五组顶部对应的纵轴数据.