题目内容
在同一平面直角坐标系中,函数f(x)=lg(x+1)的图象与函数g(x)=lg(-x+1)的图象关于( )
| A、原点对称 | B、x轴对称 |
| C、直线y=x对称 | D、y轴对称 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:易知g(x)=f(-x),由f(-x)与f(x)的图象间的关系可得g(x)与f(x)的图象关系.
解答:
解:f(-x)=lg(-x+1)=g(x),
因为f(-x)与f(x)的图象关于y轴对称,
所以f(x)与g(x)的图象关于y轴对称.
故选:D.
因为f(-x)与f(x)的图象关于y轴对称,
所以f(x)与g(x)的图象关于y轴对称.
故选:D.
点评:本题主要考查函数图象的对称变换,一般地,函数y=f(x)与函数y=f(-x)的图象关于直线y轴对称.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
已知二次函数y=x2+mx+4,当x∈R时,恒有y>0,则m的取值范围是( )
| A、(0,2) |
| B、(-2,2) |
| C、(-4.4) |
| D、(-2,0) |
已知 f(x)=|lgx|,若0<a<1<b且f(a)=f(b),则log2(1+ab)的值为( )
| A、0 | B、1 | C、-1 | D、不确定 |
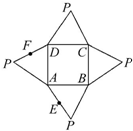 如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论: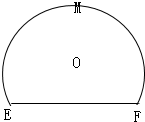 如图,一块弓形薄铁片EAF,点M为
如图,一块弓形薄铁片EAF,点M为