题目内容

在△ABC中，角A、B、C所对的边分别为a、b、c．若acosA=bsinB，则，sinAcosA+cos2A=（　　）
A、-
1
2
B、
1
2
C、-1
D、1
考点：正弦定理
专题：解三角形
分析：利用三角形中的正弦定理，将已知等式中的边用三角形的角的正弦表示，代入要求的式子，利用三角函数的平方关系求出值．
解答： 解：△ABC中，∵acosA=bsinB，由正弦定理得sinAcosA=sinBsinB，
∴sinAcosA+cos2B=sin2B+cos2B=1，
故选：D．
点评：本题考查三角形中的正弦定理、余弦定理、三角函数的平方关系，属于基础题．
练习册系列答案
相关题目
设实数a，b满足2a+b=9．
（i）若|9-b|+|a|＜3，求x的取值范围；
（ii）若a，b＞0，且z=a2b，求z的最大值．
若A（-1，0），B（0，
3
），C（3，0），动点D满足
|CD|
=1，则|
OA
+
OB
+
OD
|的最大值是
 
．
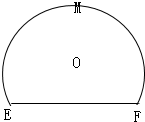如图，一块弓形薄铁片EAF，点M为
EF
的中点，其所在圆O的半径为4dm（圆心O在弓形EMF内）．∠EOF=
2π
3
，将弓形薄铁片截成尽可能大的矩形铁片ABCD（不计损耗）．AD∥EF且A、D在
EF
上，设∠AOD=2θ．
（1）求矩形铁片ABCD的面积与关于θ的函数解析式；
（2）当裁出的矩形铁片ABCD的面积最大时，求cosθ的值．
数列{an}中，a1=2，a2=7，an+2是anan+1的个位数字，Sn是{an}的前n项和，则S242-7a7=
 
．
①求函数f（x）=
4x-x2
的定义域与值域；
②计算lg4+2lg5+eln2+log 
3
3
3
．
设m，n是空间两条直线，α，β是空间两个平面，有下列四个命题：
①当m?α时，“n∥α”是“m∥n”的必要不充分条件；
②当m?α时，“m⊥β”是“α⊥β”的充分不必要条件；
③当n⊥α时，“n⊥β”是“α∥β”成立的充要条件；
④当m?α时，“n⊥α”是“m⊥n”的充分不必要条件；
以上四个命题正确的是
 
．
已知数列{an}的前n项和为Sn，若Sn=3an+2n．
（1）求证：数列{an-2}是等比数列． 
（2）若bn=n×（an-2），求数列{bn}的前n项和Tn．
在△ABC中A（2，4），B（0，-2），C（-2，3）．
（Ⅰ）求AB边垂直平分线所在直线方程；
（Ⅱ）求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网