题目内容
设随机变量X～N（μ，σ2），则η=ax+b服从（ ）
| A、N（μ，σ2） | ||||
| B、N（aμ+b，a2σ2） | ||||
| C、N（0，1） | ||||
D、N（
|
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：由随机变量X～N（μ，σ2），可得η=ax+b的期望为aμ+b，方差为a2σ2，即可得出结论．
解答：
解：∵随机变量X～N（μ，σ2），
∴η=ax+b的期望为aμ+b，方差为a2σ2，
∴η=ax+b服从N（aμ+b，a2σ2）．
故选：B．
∴η=ax+b的期望为aμ+b，方差为a2σ2，
∴η=ax+b服从N（aμ+b，a2σ2）．
故选：B．
点评：本题考查正态分布曲线的特点及曲线所表示的意义，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
若C
=C
，则n=（ ）
2n-5 11 |
n+1 11 |
| A、5 | B、6 | C、5或2 | D、5或6 |
若函数f（x）满足f（x）+1=
，当x∈[0，1]时，f（x）=x，若在区间（-1，1]上，方程f（x）-mx-2m=0有两个实数解，则实数m的取值范围是（ ）
| 1 |
| f(x+1) |
A、0＜m≤
| ||
B、0＜m＜
| ||
C、
| ||
D、
|
若双曲线C：4x2-y2=λ（λ＞0）与抛物线y2=4x的准线交于A，B两点，且|AB|=2
，则λ的值是（ ）
| 3 |
| A、1 | B、2 | C、4 | D、13 |
若函数f（x）=x3-ax2+4在（0，2）内单调递减，则实数a的取值范围为（ ）
| A、[3，+∞） |
| B、{3} |
| C、（-∞，3] |
| D、（0，3） |
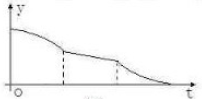
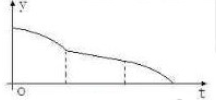
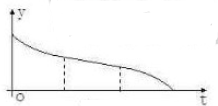
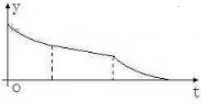
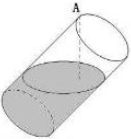一空的圆柱体容器直径小于母线长斜放，将容器斜放，使圆柱的母线与水平面成45°角，现于这种状态下由容器的最高点A处匀速地灌油，如图，则点A到油平面的距离y与灌水时间t的函数图象大致为（ ）
