Question

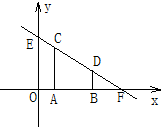如图，在平面直角坐标系中，CA⊥x轴于点A（1，0），DB⊥x轴于点B（3，0），直线CD与x轴、y轴分别交于点F、E，S_{四边形ABCD}=4．
（1）若直线CD的解析式为y=kx+3，求k的值；
（2）在（1）条件下，试探索在x轴正半轴上存在几个点P，使△EPF为等腰三角形，并求出这些点的坐标．

Answer 1

考点：直线的一般式方程

专题：直线与圆

分析：（1）由已知可得|AB|=2，由于S_{四边形ABCD}=

1

2

（|AC|+|BD|）×2=4，可得|AC|+|BD|=4．设C（1，y₁），D（3，y₂），代入y=kx+3，即可得出k．
（2）由两种情况：一种是线段EF的垂直平分线与x轴的正半轴的交点，另一种是|FP|=|FE|，点P在F点的右边．

解答： 解：（1）∵A（1，0）B（3，0），
∴|AB|=2，
∵S_{四边形ABCD}=

1

2

（|AC|+|BD|）×2=4，
∴|AC|+|BD|=4．
  设C（1，y₁），D（3，y₂），
∵y=kx+3，
∴y₁=k+3，y₂=3k+3，
∴y₁+y₂=4k+6=4，
解得k=-

1

2

．
（2）有2个．
①当点P在线段OF上时，在y=-

1

2

x+3中，令y=0得x=6
∴F（6，0），E（0，3）．
线段EF的中点(3，

3

2

)．
∴线段EF的垂直平分线的方程为：y-

3

2

=2(x-3)，
令y=0，解得x=

9

4

，
∴点P（

9

4

，0）．
②当点P在点F右边时，
∵|FP|=|EF|=

32+62

=3

5

∴|OP|=|OF|+|FP|=6+3

5

，此时P（6+3

5

，0）．
综上可得：P（

9

4

，0）或P（6+3

5

，0）．

点评：本题考查了直线的方程及其应用、梯形的面积计算公式、线段的垂直平分线、等腰三角形的性质，考查了推理能力与计算能力，属于中档题．