题目内容
设x，y满足
，则z=2x+3y的最大值是 ．
|
考点：简单线性规划
专题：数形结合,不等式的解法及应用
分析：由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，求得最优解的坐标，代入目标函数得答案．
解答：
解：由约束条件
作出可行域如图，
联立
，解得B（2，3），
化目标函数z=2x+3y为y=-
x+
，
由图可知，当直线y=-
x+
过点B（2，3）时z最大，等于2×2+3×3=13．
故答案为：13．
|
联立
|
化目标函数z=2x+3y为y=-
| 2 |
| 3 |
| z |
| 3 |
由图可知，当直线y=-
| 2 |
| 3 |
| z |
| 3 |
故答案为：13．
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，考查了数学转化思想方法，是中档题．
练习册系列答案
相关题目
设i的虚数单位，复数
为纯虚数，则实数b的值为（ ）
| 1+bi |
| 1+i |
| A、0 | B、1 | C、-1 | D、±1 |
若O为△ABC所在平面内任一点，且满足（
-
）•（
+
-2
）=0，则△ABC一定是（ ）
| OB |
| OC |
| OB |
| OC |
| OA |
| A、正三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
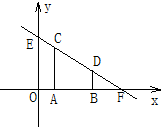如图，在平面直角坐标系中，CA⊥x轴于点A（1，0），DB⊥x轴于点B（3，0），直线CD与x轴、y轴分别交于点F、E，S四边形ABCD=4．