题目内容
若f(x)在R上为奇函数,当x>0时,f(x)=x2+x,则f(x)= .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:先设x<0,则-x>0,代入f(x)=x2+x并进行化简,再利用f(x)=-f(-x)进行求解.
解答:
解:设x<0,则-x>0,
∵当x>0时,f(x)=x2+x,
∴f(-x)=(-x)2+(-x)=x2-x,
∵f(x)是定义在R上的奇函数,f(0)=0,
∴f(x)=-x2+x,
f(x)=
故答案为:
.
∵当x>0时,f(x)=x2+x,
∴f(-x)=(-x)2+(-x)=x2-x,
∵f(x)是定义在R上的奇函数,f(0)=0,
∴f(x)=-x2+x,
f(x)=
|
故答案为:
|
点评:本题考查了函数奇偶性的应用,即根据奇偶性对应的关系式,将所求的函数解析式进行转化,转化到已知范围内进行求解,考查了转化思想.

练习册系列答案
相关题目
已知函数f(x)为奇函数,且x>0时,f(x)=x(1+x3),则x<0时,f(x)=( )
| A、x(1-x3) |
| B、-x(1+x3) |
| C、-x(1-x3) |
| D、x(1+x3) |
设x,y满足约束条件
,若目标函数z=ax+by(a>0,b>0)的最大值为12,则直线ax+by+1=0必过定点( )
|
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(-
|
设函数f(x)是偶函数,当x≥0时,f(x)=2x-4,则不等式f(x-2)>0的解集为( )
| A、{x|x<-2或x>4} |
| B、{x|x<0或x>4} |
| C、{x|x<0或x>6} |
| D、{x|x<-2或x>2} |
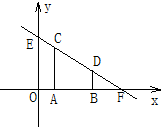 如图,在平面直角坐标系中,CA⊥x轴于点A(1,0),DB⊥x轴于点B(3,0),直线CD与x轴、y轴分别交于点F、E,S四边形ABCD=4.
如图,在平面直角坐标系中,CA⊥x轴于点A(1,0),DB⊥x轴于点B(3,0),直线CD与x轴、y轴分别交于点F、E,S四边形ABCD=4. 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则f(0)=
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则f(0)=