Question

2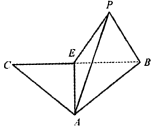．等腰三角形ABC，E为底边BC的中点，沿AE折叠，如图，将C折到点P的位置，使P-AE-C为120°，设点P在面ABE上的射影为H．
（1）证明：点H为EB的中点；
（2）若$AB=AC=2\sqrt{2}，AB⊥AC$，求H到平面ABP的距离．

Answer 1

分析 （1）推导出AE⊥面EPB，∠CEP为二面角C-AE-P的平面角，从而EH=$\frac{1}{2}$EP=$\frac{1}{2}$EB，由此能证明H为EB的中点．
（2）过H作HM⊥AB于M，连PM，过H作HN⊥PM于N，连BN，则HN为H到平面ABP的距离，由此能求出结果．

解答 证明：（1）依题意，AE⊥BC，则AE⊥EB，AE⊥EP，EB∩EP=E．
∴AE⊥面EPB．
故∠CEP为二面角C-AE-P的平面角，则点P在面ABE上的射影H在EB上．
由∠CEP=120°，得∠PEB=60°．…（3分）
∴EH=$\frac{1}{2}$EP=$\frac{1}{2}$EB．
∴H为EB的中点．…（6分）
解：（2）过H作HM⊥AB于M，连PM，过H作HN⊥PM于N，连BN，
则有三垂线定理得AB⊥面PHM．
即面PHM⊥面PAB，
∴HN⊥面PAB．∴HN为H到平面ABP的距离．…（9分）
依题意，BE=$\frac{1}{2}BC=2$．BH=$\frac{1}{2}BE=1$．
在△HMB中，HM=$\frac{\sqrt{2}}{2}$，
在△EPB中，PH=$\sqrt{3}$，
∴在Rt△PHM中，HN=$\frac{\sqrt{21}}{7}$．…（12分）

点评 本题考查点为线段中点的证明，考查点到平面的距离的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．