题目内容
7.已知正四面体棱长为4$\sqrt{2}$,则此正四面体外接球的表面积为( )| A. | 36π | B. | 48π | C. | 64π | D. | 72π |
分析 将正四面体补成一个正方体,正四面体的外接球的直径为正方体的对角线长,即可得出结论.
解答 解:将正四面体补成一个正方体,则正方体的棱长为4,正方体的对角线长为4$\sqrt{3}$,
∵正四面体的外接球的直径为正方体的对角线长,
∴外接球的表面积的值为$4π•(2\sqrt{3})^{2}$=48π.
故选B.
点评 本题考查球的内接多面体等基础知识,考查运算求解能力,考查逻辑思维能力,属于基础题.

练习册系列答案
相关题目
2.在空间中,下列命题正确的是( )
| A. | 如果直线m∥平面α,直线n?α内,那么m∥n | |
| B. | 如果平面α⊥平面β,任取直线m?α,那么必有m丄β | |
| C. | 若直线m∥平面α,直线n∥平面α,则m∥n | |
| D. | 如果平面a外的一条直线m垂直于平面a内的两条相交直线,那么m⊥α |
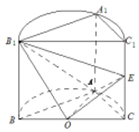 如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4
如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4 已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是线段CC1的中点,连接AE,B1E,AB1,B1C,BC1,得到的图形如图所示.
已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是线段CC1的中点,连接AE,B1E,AB1,B1C,BC1,得到的图形如图所示.