题目内容
4.已知三条直线m,n,l,三个平面α,β,γ,下面说法正确的是( )| A. | $\left.\begin{array}{l}{α⊥γ}\\{β⊥γ}\end{array}\right\}$⇒α∥β | B. | $\left.\begin{array}{l}{m⊥l}\\{n⊥l}\end{array}\right\}$⇒m∥n | C. | $\left.\begin{array}{l}{m∥β}\\{l⊥m}\end{array}\right\}$⇒l∥β | D. | $\left.\begin{array}{l}{m∥n}\\{n⊥γ}\end{array}\right\}$⇒m⊥γ |
分析 在A中,α与β相交或平行;在B中,m与n相交、平行或异面;在C中,l与β相交、平行或l?β;在D中,由线面垂直的判定定理得m⊥γ.
解答 解:三条直线m,n,l,三个平面α,β,γ,知:
在A中,$\left.\begin{array}{l}{α⊥γ}\\{β⊥γ}\end{array}\right\}$⇒α与β相交或平行,故A错误;
在B中,$\left.\begin{array}{l}{m⊥l}\\{n⊥l}\end{array}\right\}$⇒m与n相交、平行或异面,故B错误;
在C中,$\left.\begin{array}{l}{m∥β}\\{l⊥m}\end{array}\right\}$⇒l与β相交、平行或l?β,故C错误;
在D中,$\left.\begin{array}{l}{m∥n}\\{n⊥γ}\end{array}\right\}$⇒m⊥γ,由线面垂直的判定定理得m⊥γ,故D正确.
故选:D.
点评 本题考查命题真判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.直线y=5与y=-1在区间$[{0\;,\;\;\frac{4π}{ω}}]$上截曲线$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$所得弦长相等且不为零,则下列描述正确的是( )
| A. | $m≤\frac{3}{2}\;,\;\;n=\frac{5}{2}$ | B. | m≤3,n=2 | C. | $m>\frac{3}{2}$ | D. | m>3,n=2 |
13.等差数列{an}的前项和为Sn,若a3+a8+a13=21,则S15的值是( )
| A. | 105 | B. | 120 | C. | 56 | D. | 84 |
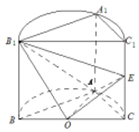 如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4
如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4 已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是线段CC1的中点,连接AE,B1E,AB1,B1C,BC1,得到的图形如图所示.
已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是线段CC1的中点,连接AE,B1E,AB1,B1C,BC1,得到的图形如图所示.