题目内容
2.△ABC内角A,B,C的对边分别为a,b,c,若a,b,c成等差数列,且sinA,sinB,sinC成等比数列,则角B=$\frac{π}{3}$.分析 由已知及等差数列,等比数列的性质可得2b=a+c,sin2B=sinAsinC,由正弦定理可得b2=ac,整理解得a=c,从而可求a=b=c,进而可求B的值.
解答 解:∵a,b,c成等差数列,且sinA,sinB,sinC成等比数列,
∴2b=a+c,sin2B=sinAsinC,即b2=ac,
∴(a+c)2=4ac,整理可得:(a-c)2=0,解得a=c,
∴b2=ac=a2=c2,可得:a=b=c,
∴B=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题主要考查了等差数列和等比数列在解三角形中的应用.等差中项和等比中项的利用是解本题的关键,属于基础题.

练习册系列答案
相关题目
12.某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人.
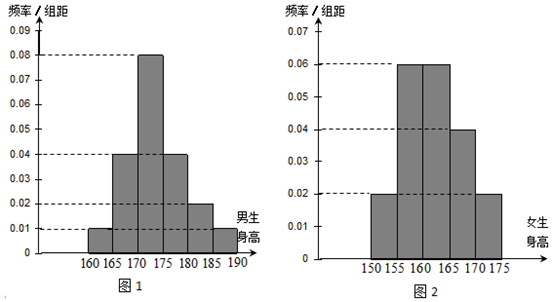
(1)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式及参考数据如下:${k^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$

(1)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
参考公式及参考数据如下:${k^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.025 | 0.610 | 0.005 | 0.001 |
| k0 | 5.024 | 4.635 | 7.879 | 10.828 |