题目内容
9.设命题p:?x0∈(0,+∞),x0+$\frac{1}{{x}_{0}}$>3;命题q:?x∈(2,+∞),x2>2x,则下列命题为真的是( )| A. | p∧(¬q) | B. | (¬p)∧q | C. | p∧q | D. | (¬p)∨q |
分析 先判断命题p、q的真假,再利用复合命题真假的判定方法即可得出.
解答 解:命题p:?x0∈(0,+∞),x0+$\frac{1}{{x}_{0}}$>3,是真命题,例如取x0=4;
命题q:?x∈(2,+∞),x2>2x,是假命题,取x=4时,x2=2x.
则下列命题为真的是p∧(¬q).
故选:A.
点评 本题考查了函数的性质、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.已知$\vec a,\vec b$均为单位向量,且$(2\vec a+\vec b)•(\vec a-2\vec b)=-\frac{{3\sqrt{3}}}{2}$,则向量$\vec a,\vec b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
20.四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,若该四棱锥的所有顶点都在体积为$\frac{9π}{2}$的同一球面上,则PA的长为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
4.已知曲线C:y=ex和直线l:ax+by=0,若直线l上有且只有两个关于y轴的对称点在曲线C上,则$\frac{b}{a}$的取值范围是( )
| A. | (-∞,-e) | B. | (-∞,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$) | D. | (e,+∞) |
18.若实数x,y满足约束条件$\left\{\begin{array}{l}x-1≥0\\ x-y≤0\\ x+y-6≤0\end{array}\right.$,则x-2y的最大值为( )
| A. | -9 | B. | -3 | C. | -1 | D. | 3 |
19.(文)已知是虚数单位,则$\frac{3+i}{1-i}$=( )
| A. | 1+2i | B. | 2+i | C. | -1+i | D. | -1-i |
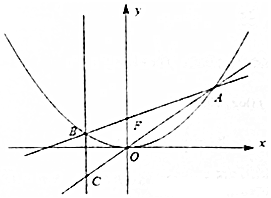 已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.
已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.