题目内容
19.(文)已知是虚数单位,则$\frac{3+i}{1-i}$=( )| A. | 1+2i | B. | 2+i | C. | -1+i | D. | -1-i |
分析 直接由复数代数形式的乘除运算化简$\frac{3+i}{1-i}$得答案.
解答 解:$\frac{3+i}{1-i}$=$\frac{(3+i)(1+i)}{(1-i)(1+i)}=\frac{2+4i}{2}=1+2i$,
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
9.设命题p:?x0∈(0,+∞),x0+$\frac{1}{{x}_{0}}$>3;命题q:?x∈(2,+∞),x2>2x,则下列命题为真的是( )
| A. | p∧(¬q) | B. | (¬p)∧q | C. | p∧q | D. | (¬p)∨q |
10.给出如下四个命题:①e${\;}^{\frac{2}{e}}$>2②ln2>$\frac{2}{3}$③π2<3π④$\frac{ln2}{2}$<$\frac{lnπ}{π}$,正确的命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.设函数$f(x)=\frac{{6sinxcosx-4cosx{{sin}^3}x}}{{2\sqrt{2}+sin(2x+\frac{π}{4})+cos(2x+\frac{π}{4})}}$,则( )
| A. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递增 | B. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递增 | ||
| C. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递减 | D. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递减 |
8.已知曲线C1:y2=tx (y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+l-1也相切,则t的值为( )
| A. | 4e2 | B. | 4e | C. | $\frac{e^x}{4}$ | D. | $\frac{e}{4}$ |
2.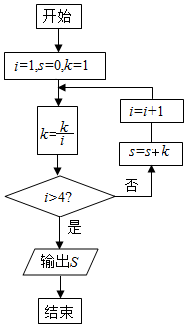 阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
 阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
阅读如图的程序框图,运行相应的程序,则输出的S的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{41}{24}$ | D. | $\frac{103}{60}$ |
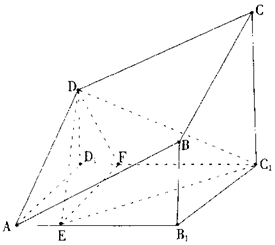 如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.
如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.