题目内容
18.若实数x,y满足约束条件$\left\{\begin{array}{l}x-1≥0\\ x-y≤0\\ x+y-6≤0\end{array}\right.$,则x-2y的最大值为( )| A. | -9 | B. | -3 | C. | -1 | D. | 3 |
分析 作出不等式组表示的平面区域;作出目标函数对应的直线;结合图象知当直线过B(2,3)时,z最小,当直线过A时,z最大.
解答 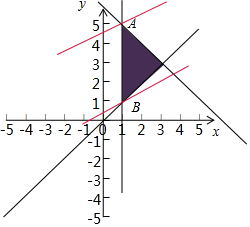 解:画出不等式$\left\{\begin{array}{l}x-1≥0\\ x-y≤0\\ x+y-6≤0\end{array}\right.$表示的平面区域:
解:画出不等式$\left\{\begin{array}{l}x-1≥0\\ x-y≤0\\ x+y-6≤0\end{array}\right.$表示的平面区域:
将目标函数变形为z=x-2y,作出目标函数对应的直线,
直线过B时,直线的纵截距最小,z最大,
由:$\left\{\begin{array}{l}{x=1}\\{x=y}\end{array}\right.$,
可得B(1,1),z最大值为-1;
故选:C.
点评 本题考查画不等式组表示的平面区域、考查数形结合求函数的最值.

练习册系列答案
相关题目
8.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,过F2的直线交双曲线右支于P,Q两点,且PQ⊥PF1,若$|PQ|=\frac{5}{12}|P{F_1}|$,则双曲线离心率e为( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{37}}}{2}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{37}}}{5}$ |
9.设命题p:?x0∈(0,+∞),x0+$\frac{1}{{x}_{0}}$>3;命题q:?x∈(2,+∞),x2>2x,则下列命题为真的是( )
| A. | p∧(¬q) | B. | (¬p)∧q | C. | p∧q | D. | (¬p)∨q |
6.设不等式组$\left\{\begin{array}{l}3x+y-10≥0\\ x+3y-6≤0\end{array}\right.$表示的平面区域为D,若函数y=logax(a>1)的图象上存在区域D上的点,则实数a的取值范围是( )
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
10.给出如下四个命题:①e${\;}^{\frac{2}{e}}$>2②ln2>$\frac{2}{3}$③π2<3π④$\frac{ln2}{2}$<$\frac{lnπ}{π}$,正确的命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.已知曲线C1:y2=tx (y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+l-1也相切,则t的值为( )
| A. | 4e2 | B. | 4e | C. | $\frac{e^x}{4}$ | D. | $\frac{e}{4}$ |
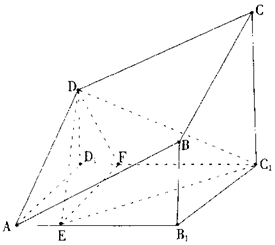 如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.
如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.