题目内容
5.已知函数f ( x)=ax3+bx2+cx+d 的图象如图所示,则$\frac{b+1}{a+1}$的取值范围是( )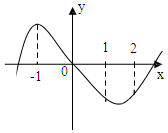
| A. | (-$\frac{3}{2}$,$\frac{1}{2}$ ) | B. | (-$\frac{2}{5}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$) | D. | (-$\frac{3}{2}$,1) |
分析 利用函数以及导数的图象,推出a,b 的不等式组,然后求解即可.由图象可知:经过原点,可得f(0)=0=d,即f(x)=ax3+bx2+cx..由图象可得:函数f(x)在[-1,1]上单调递减,函数f(x)在x=-1处取得极大值.可得f′(x)≤0在[-1,1]上恒成立,且f′(-1)=0.利用且f′(1)<0,f′(2)>0即可得到b<0,3a+2b>0,设k=$\frac{b+1}{a+1}$,求k的最值,进而得出结论.
解答  解:由图象可知:经过原点,∴f(0)=0=d,
解:由图象可知:经过原点,∴f(0)=0=d,
∴f(x)=ax3+bx2+cx.
由图象可得:函数f(x)在[-1,1]上单调递减,函数f(x)在x=-1处取得极大值.
∴f′(x)=3ax2+2bx+c≤0在[-1,1]上恒成立,且f′(-1)=0.
得到3a-2b+c=0,即c=2b-3a,
∵f′(1)=3a+2b+c<0,
∴4b<0,即b<0,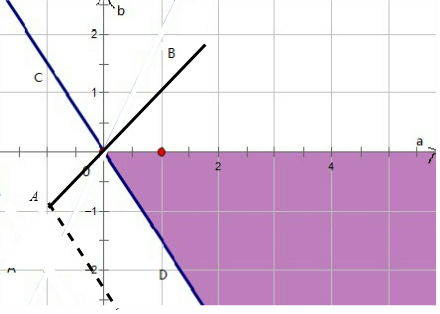
∵f′(2)=12a+4b+c>0,
∴3a+2b>0,
设k=$\frac{b+1}{a+1}$,
建立如图所示的坐标系,则点A(-1,-1),
则k=$\frac{b+1}{a+1}$式中变量a、b满足下列条件$\left\{\begin{array}{l}{3a+2b>0}\\{b<0}\end{array}\right.$,
作出可行域如图:
∴k的最大值就是kAO=1,k的最小值就是kCD,
而kCD就是直线3a+2b=0的斜率,kCD=-$\frac{3}{2}$,
∴-$\frac{3}{2}$<k<1.
故选:D.
点评 本题综合考查了利用导数研究函数的单调性极值、数形结合等基础知识与基本方法.

练习册系列答案
相关题目
15.我们知道,在长方形ABCD中,如果设AB=a,BC=b,那么长方形ABCD的外接圆的半径R满足4R2=a2+b2,类比上述结论,在长方体ABCD-A1B1C1D1中,如果设AB=a,AD=b,AA1=c,那么长方体ABCD-A1B1C1D1的外接球的半径R满足的关系式是( )
| A. | 4R2=a3+b3+c3 | B. | 8R2=a2+b2+c2 | C. | 8R3=a3+b3+c3 | D. | 4R2=a2+b2+c2 |
10.命题“?x>0,$\frac{x-2}{x}$≥0”的否定是( )
| A. | ?x≤0,$\frac{x-2}{x}$<0 | B. | ?x>0,$\frac{x-2}{x}$<0 | C. | ?x>0,0≤x<2 | D. | ?x>0,0<x<2 |
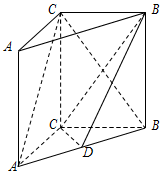 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.求证:
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.求证: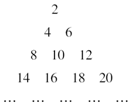 把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).
把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).