题目内容
8．函数 f （ x）=$\frac{x}{lnx}$（ x＞1）单调递减区间是（ ）| A． | （1，+∞） | B． | （1，e2） | C． | （e，+∞） | D． | （1，e） |
分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可．
解答 解：f′（x）=$\frac{lnx-1}{{（lnx）}^{2}}$，
令f′（x）＜0，解得：1＜x＜e，
故f（x）在（1，e）递减，
故选：D．
点评 本题考查了函数的单调性问题，考查导数的应用，是一道基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
18．下列求导结果正确的是（ ）
| A． | （a-x2）′=1-2x | B． | （2$\sqrt{{x}^{3}}$）′=3$\sqrt{x}$ | C． | （cos60°）′=-sin60° | D． | [ln（2x）]′=$\frac{1}{2x}$ |
3．若$α∈（\frac{π}{2}，π）$，且$3cos2α=sin（\frac{π}{4}-α）$，则cos2α的值为（ ）
| A． | $-\frac{{\sqrt{35}}}{18}$ | B． | $\frac{{\sqrt{35}}}{18}$ | C． | $\frac{17}{18}$ | D． | $-\frac{17}{18}$ |
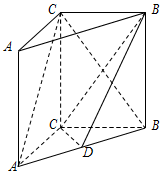如图，在三棱柱ABC-A1B1C1中侧棱垂直于底面，AC⊥BC，点D是AB的中点．求证：
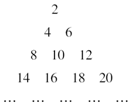把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵，记M（r，t）表示该数阵中第r行的第t个数，则数阵中的数2 018对应于（45，19）．
18．设正三棱锥A-BCD内接于球O，BC=1，E为AB的中点，AC⊥DE，则球的半径为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{6}}}{4}$ | D． | $\frac{{\sqrt{10}}}{4}$ |