题目内容
17.函数的$f(x)={2^{{x^2}+x-3}}$单调增区间是(-$\frac{1}{2}$,+∞).分析 令t=x2+x-3,则f(x)=g(t)=2t,本题即求函数t的增区间,再利用二次函数的性质得出结论.
解答 解:令t=x2+x-3=${(x+\frac{1}{2})}^{2}$-$\frac{13}{4}$,故函数t的图象的对称轴为x=-$\frac{1}{2}$,f(x)=g(t)=2t,
故f(x)的增区间即为函数t的增区间,而函数t的增区间为$({-\frac{1}{2},+∞})$,
故答案为:(-$\frac{1}{2}$,+∞).
点评 本题主要考查复合函数的单调性,指数函数、二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.将y=cosx的图象上的所有点的纵坐标不变,横坐标缩小到原来的一半,然后再将图象沿x轴负方向平移$\frac{π}{4}$个单位,则所得图象的解析式为( )
| A. | y=sinx | B. | y=-sin2x | C. | $y=cos({2x+\frac{π}{4}})$ | D. | $y=cos({\frac{x}{2}+\frac{π}{4}})$ |
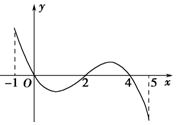 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题: