题目内容
13.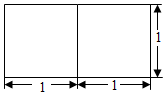 若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )
若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | 2 |
分析 根据正三棱柱的主视图确定出三棱柱的底面边长与高,即可求出侧面积.
解答 解:由主视图知:三棱柱是以底面边长为2,高为1的正三棱柱,
则侧面积为3×2×1=6,
故选:C.
点评 此题考查了由三视图求面积、体积,确定出三棱柱的底面边长与高是解本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
3.点F为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a,b>0)的焦点,过点F的直线与双曲线的一条渐近线垂直且交于点A,与另一条渐近线交于点B.若3$\overrightarrow{AF}$+$\overrightarrow{BF}$=0,则双曲线C的离心率是( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
1.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=ex | B. | y=lnx2 | C. | y=$\sqrt{x}$ | D. | y=sinx |
18.已知S1=$\int_1^2$xdx,S2=$\int_1^2$exdx,S3=$\int_1^2$x2dx,则S1,S2,S3的大小关系为( )
| A. | S1<S2<S3 | B. | S1<S3<S2 | C. | S3<S2<S1 | D. | S2<S3<S1 |
5.已知球O的半径为1,A,B,C三点都在球面上,且∠AOB=∠AOC=∠BOC=90°,则球心O到平面ABC的距离为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
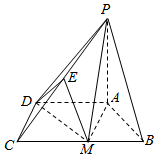 已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.
已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.