题目内容
4.已知数列{an}中,a1=2,当n≥2时,an-n=an-1+$\frac{2}{\sqrt{n}+\sqrt{n-1}}$,求an.分析 利用数列的递推关系式,通过数列求和求解即可.
解答 解:数列{an}中,a1=2,当n≥2时,an-n=an-1+$\frac{2}{\sqrt{n}+\sqrt{n-1}}$,
可得a1=2
a2-2=a1+$\frac{2}{\sqrt{2}+1}$,
a3-3=a2+$\frac{2}{\sqrt{3}+\sqrt{2}}$,
a4-4=a3+$\frac{2}{\sqrt{4}+\sqrt{3}}$,
…
an-n=an-1+$\frac{2}{\sqrt{n}+\sqrt{n-1}}$,
将上述各式相加可得:
an-(2+3+4+…+n)=2+$\frac{2}{\sqrt{2}+1}$+$\frac{2}{\sqrt{3}+\sqrt{2}}$+$\frac{2}{\sqrt{4}+\sqrt{3}}$+…+$\frac{2}{\sqrt{n}+\sqrt{n-1}}$,
即:an-$\frac{(n+2)(n-1)}{2}$=2(1+$\sqrt{2}-1$+$\sqrt{3}-\sqrt{2}$$+\sqrt{4}-\sqrt{3}$+…+$\sqrt{n}$$-\sqrt{n-1}$)=2$\sqrt{n}$.
an=$\frac{(n+2)(n-1)}{2}$+2$\sqrt{n}$.
点评 本题考查数列的递推关系式的应用,数列求和,考查计算能力,转化思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在k进制中,十进制数103记为87,则k等于( )
| A. | 6 | B. | 12 | C. | 14 | D. | 16 |
13.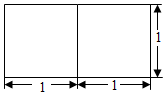 若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )
若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )
 若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )
若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | 2 |