题目内容
5.已知球O的半径为1,A,B,C三点都在球面上,且∠AOB=∠AOC=∠BOC=90°,则球心O到平面ABC的距离为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 判断三棱锥的形状,利用三棱锥的体积求解球心O到平面ABC的距离.
解答 解:由题意可知,棱锥O-ABC是正方体的一个角,正方体的棱长为:1,AB=BC=AC=$\sqrt{2}$,△ABC是正三角形,
S△ABC=$\frac{\sqrt{3}}{4}×(\sqrt{2})^{2}$=$\frac{\sqrt{3}}{2}$,V0-ABC=VC-AOB,球心O到平面ABC的距离为h,
可得:$\frac{1}{3}×\frac{\sqrt{3}}{2}×h$=$\frac{1}{3}×\frac{1}{2}×1×1×1$,
可得:h=$\frac{\sqrt{3}}{3}$.
故选:B.
点评 本题考查点到平面的距离的求法,等体积法的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
13.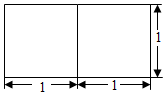 若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )
若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )
 若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )
若一个正三棱柱的主视图是如图所示的两个并列的正方形,则其侧面积等于( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | 2 |
10.设m=${∫}_{0}^{1}$exdx,n=${∫}_{1}^{e}$$\frac{1}{x}$dx,则m与n的大小关系为( )
| A. | m<n | B. | m≤n | C. | m>n | D. | m≥n |
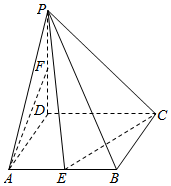 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E,F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E,F分别为AB和PD的中点.