题目内容
11.已知双曲线y2-4x2=16上一点M到一个焦点的距离等于2,则点M到另一个焦点的距离为10.分析 将双曲线的方程化为标准方程,可得a=4,设|MF1|=2,运用双曲线的定义可得||MF1|-|MF2||=2a=8,计算即可得到所求距离.
解答 解:双曲线y2-4x2=16即为
$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{4}$=1,
可得a=4,
设双曲线的两焦点为F1,F2,
由题意可设|MF1|=2,
由双曲线的定义可得||MF1|-|MF2||=2a=8,
即有|2-|MF2||=8,
解得|MF2|=10或-6(舍去).
故答案为:10.
点评 本题考查双曲线的一点到焦点的距离,注意运用双曲线的定义,考查运算能力,属于基础题.

练习册系列答案
相关题目
16.已知菱形ABCD中,AC=2,BD=4,E,F分别在AB,AD上,且关于直线AC对称,则$\overrightarrow{BF}•\overrightarrow{CE}$的最大值为( )
| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{5}{6}$ |
14.$\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{DB}$=( )
| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{BD}$ |
1.与椭圆$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1有相同的焦点,且经过点P($\sqrt{2}$,-$\sqrt{2}$)的双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
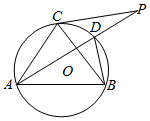 如图,圆O是△ABC的外接圆,点D是劣弧$\widehat{BC}$的中点,连结AD并延长,与以C为切点的切线交于点P,求证:$\frac{PC}{PA}=\frac{BD}{AC}$.
如图,圆O是△ABC的外接圆,点D是劣弧$\widehat{BC}$的中点,连结AD并延长,与以C为切点的切线交于点P,求证:$\frac{PC}{PA}=\frac{BD}{AC}$.