题目内容
10.设复数z满足z(1+i)=i(i为虚数单位),则|z|=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
分析 先求出复数z,然后利用求模公式可得答案.
解答 解:由z(1+i)=i得z=$\frac{i}{1+i}$=$\frac{i(1-i)}{(1+i)(1-i)}$=$\frac{1}{2}$+$\frac{1}{2}$i,
则则|z|=$\sqrt{(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$,
故选:B
点评 本题考查复数代数形式的运算、复数求模,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.曲线$y={(\frac{1}{3})^x}$与$y={x^{\frac{1}{2}}}$的交点横坐标所在区间为( )
| A. | $(0,\;\frac{1}{3})$ | B. | $(\frac{1}{3},\;\frac{1}{2})$ | C. | $(\frac{1}{2},\;\frac{2}{3})$ | D. | $(\frac{2}{3},\;1)$ |
2.已知集合A={0,1,2,3,4},B={x|x2-2x>0},则A∩B=( )
| A. | (2,4] | B. | [2,4] | C. | {0,3,4} | D. | {3,4} |
19.设F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,若OF的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为$\frac{1}{2}|OF|$,则双曲线的离心率为( )
| A. | $2\sqrt{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
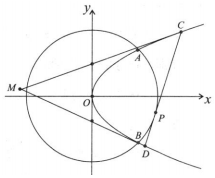 如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.
如图,抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.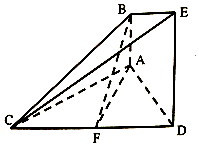 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.